Грег Иган. Статьи – Far Above The World

От переводчика:

Эту статью можно рассматривать как своеобразное приложение к рассказу Грега Игана “На развалинах” (In the Ruins), переведенному Григорием Шокиным и опубликованному на русском языке в рамках самиздат-сборника “3-адика“.

Оригинал на сайте автора: http://gregegan.net/SCIENCE/Ellipse/Ellipse.html

Что эллиптические орбиты планет могут рассказать нам об энергетических уровнях атома? Несмотря на то, что реальный атом едва ли можно сравнить с миниатюрной солнечной системой, электростатическая сила подчиняется тому же закону обратных квадратов, что и ньютоновская сила тяготения. В простейшем случае – когда речь идет об атоме водорода, состоящем из одного протона и одного электрона – особая симметрия, характерная для всех обратноквадратичных зависимостей, отчетливо проявляется в квантовомеханической версии системы. Этот факт был известен еще в эпоху становления квантовой механики, когда Вольфганг Паули воспользовался им, чтобы рассчитать энергетические уровни водорода^[1][2]. Как мы увидим далее, эта симметрия связана с поворотами в четырехмерном пространстве.

В этом приложении мы примем как данность два хорошо известных факта: что орбита, по которой единственная планета обращается вокруг звезды под действием ньютоновской гравитации, имеет форму эллипса (в частном случае это может быть окружность), и что сумма расстояний от любой точки эллипса до его фокусов является постоянной величиной. Доказательство этих утверждений можно найти на сайте автора.

Круг скоростей

Для начала мы рассмотрим планету, обращающуюся вокруг Солнца по круговой орбите. В реальности и планета, и Солнце будут, разумеется, двигаться вокруг их общего центра масс, что, однако же, почти не скажется на картине в целом. Если мы все же хотим принять это во внимание, то можем заменить массу планеты соответствующей «приведенной массой» – при этом суть вычислений остается без изменений.

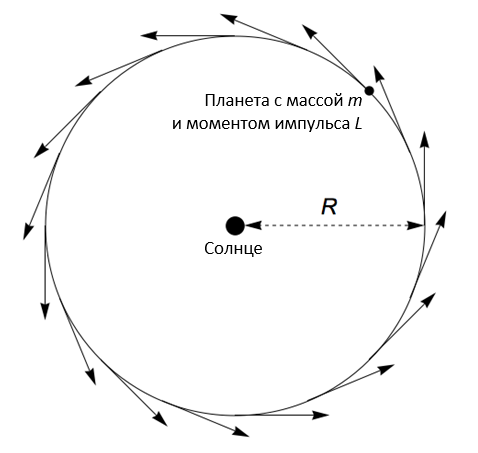
По мере вращения планеты ее вектор скорости будет менять направление, но его длина, или абсолютное значение, останется неизменным. Поэтому если мы изобразим все орбитальные векторы скорости, поместив их начала в одну точку, то получим круг.

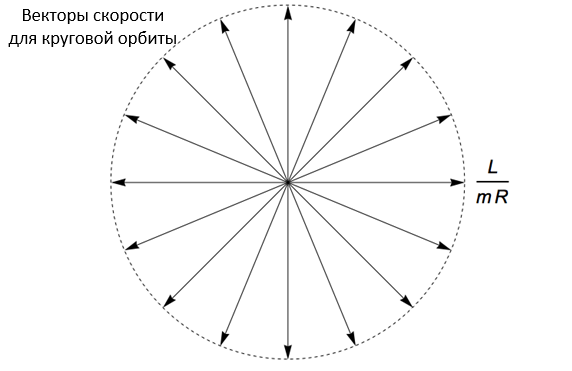
Допустим, что масса планеты равна m, а момент импульса составляет L. Чтобы найти скорость планеты, достаточно решить уравнение L = mvR. Таким образом, радиус круга скоростей равен v=L/(mR).

Предположим теперь, что планета движется по эллиптической орбите, причем расстояние в перигелии (максимальное сближение с Солнцем) равно R₁, а расстояние в афелии (максимальное отдаление от Солнца) – R₂. В отличие от предыдущего случая скорость планеты будет меняться по хожу ее орбитального движения.

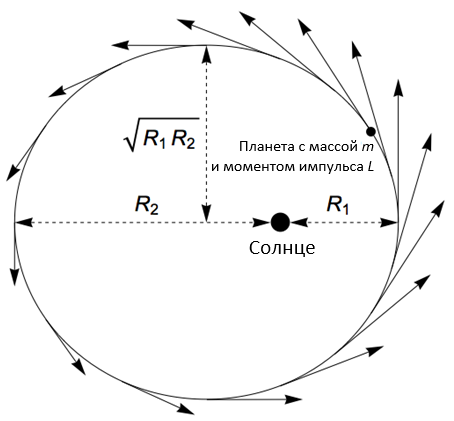
Помимо знания величин R₁ и R₂, нам пригодятся размеры большой и малой полуосей эллипса, которые по традиции обозначаются буквами a и b соответственно. Они характеризуют соответственно наибольшее и наименьшее расстояния от точек эллипса до его центра, в отличие от R₁ и R₂, равных соответственно наименьшему и наибольшему расстояниям до одного из фокусов.

Большая полуось a, очевидно равна среднему арифметическому R₁ и R₂:

$a = \cfrac{R_1 + R_2}{2}$

Менее очевидно, что малая полуось b равна среднему геометрическому тех же величин. Средним геометрическим двух чисел называется квадратный корень их произведения:

$b = \sqrt{R_1 R_2}$

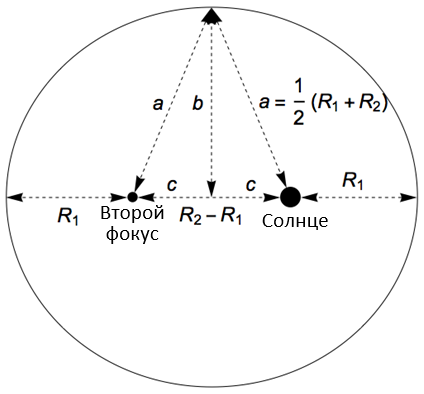
Для доказательства мы вначале заметим, что в силу симметрии второй фокус должен находиться на расстоянии R₁ от крайней левой точки эллипса, поэтому расстояние между фокусами равно R₂ – R₁. Половину расстояния от центра до любого из фокусов принято обозначать буквой c, поэтому:

$c = \cfrac{R_2 - R_1}{2}$

Далее мы воспользуемся основным свойством эллипса: сумма расстояний от любой точки на кривой до двух фокусов должна быть постоянной. Для нашего эллипса эта константа равна 2a = R₁ + R₂. Точка, равноудаленная от обоих фокусов, будет находиться от них на расстоянии a = ½(R₁ + R₂), в то время как ее расстояние до центра эллипса равно b. Применив теорему Пифагора, имеем:

$b^2 = a^2 - c^2 = (a - c)(a + c) = R_1 R_2$

Как будут выглядеть векторы скорости для такой орбиты, если мы приведем их к общему началу? Момент импульса планеты, обращающейся вокруг Солнца, равен произведению ее массы, скорости и расстояния между планетой и Солнцем, измеренным вдоль перпендикуляра к вектору скорости; это позволяет нам сразу дже определить скорость планеты для четырех точек, в которых соответствующий вектор параллелен одной из осей эллипса:

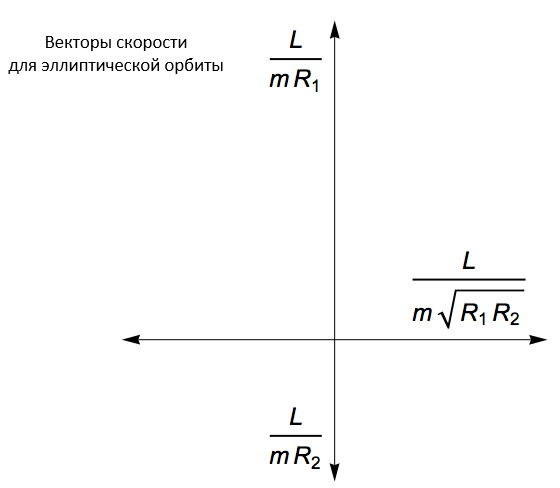
Как ни странно, эти точки лежат на одной окружности! Главное отличие от случая с круговой орбитой заключается в том, что центр круга скоростей смещен относительно общего начала векторов:

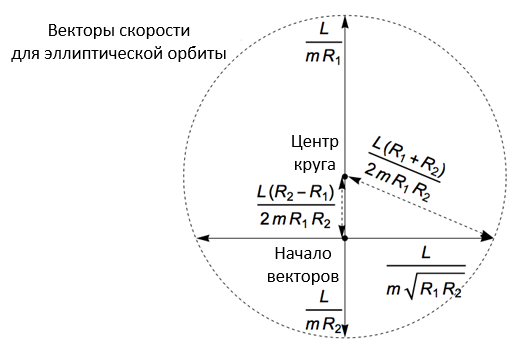
В данном случае мы просто поместили центр посередине между верхней и нижней точками, а затем, чтобы убедиться, что все точки расположены на окружности, воспользовались теоремой Пифагора и проверили, что расстояние до боковых точек совпадает с расстоянием до верхней и нижней. Это легко сделать, если мы обратим внимание на следующие моменты:

Расстояние до верхней/нижней точки = $\cfrac{L(R_1 + R_2)}{2m R_1 R_2} = \cfrac{aL}{m R_1 R_2}$

Расстояние по горизонтали до боковых точек = $\cfrac{L}{m\sqrt{R_1 R_2}} = \cfrac{bL}{m R_1 R_2}$

Расстояние по вертикали до боковых точек = $\cfrac{L(R_2 - R_1)}{2m R_1 R_2} = \cfrac{cL}{m R_1 R_2}$

Поскольку a² = b² + c², то же самое соотношение должно выполняться и для расстояний, показанных на диаграмме, так как они отличаются от a, b, c только множителем L / (m R₁ R₂).

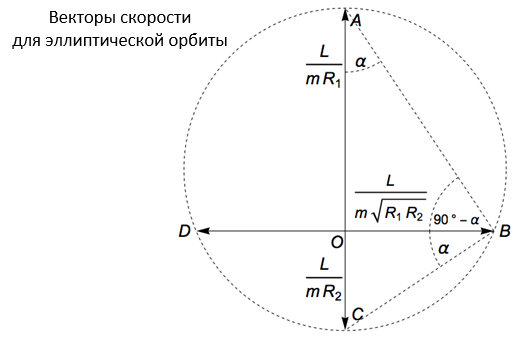
Убедиться в этом можно и другим способом: для этого нужно воспользоваться приведенной выше диаграммой, обратив внимание на то, что прямоугольные треугольники OAB и OBC характеризуются одним и тем же отношением катетов:

$\cfrac{OA}{OB} = \cfrac{\sqrt{R_1 R_2}}{R_1} = \sqrt{\cfrac{R_2}{R_1}}$

$\cfrac{OB}{OC} = \cfrac{R_2}{\sqrt{R_1 R_2}} = \sqrt{\cfrac{R_2}{R_1}}$

Другими словами, эти треугольники являются подобными, а угол OAB (обозначим его α) равен углу OBC. Отсюда следует, что угол ABC является прямым. Если мы построим окружность, проходящую через три вершины прямоугольного треугольника, то его гипотенуза окажется одним из диаметров, поэтому из соображений симметрии на той же самой окружности должен лежать и конец четвертого вектора (совпадающий с точкой D).

Доказательство того, что концы всех (а не только рассмотренной нами четверки) векторов скорости лежат на одной и той же окружности, потребует чуть больших усилий. Введя систему координат с центром в правом фокусе (т. е. там, где располагается Солнце), представим произвольную точку орбиты в виде:

$\mathbf{r}(\theta) = r(\theta) (\cos \theta, \sin \theta)$

Второй фокус будет находиться в точке (–(R₂ – R₁), 0). Таким образом, для того, чтобы сумма расстояний до двух фокусов была равна R₁ + R₂, расстояние r(θ) должно удовлетворять уравнению:

$(R_1 + R_2 - r(\theta))^2 = (r(\theta) \cos \theta + R_2 - R_1)^2 + r^2(\theta) \sin^2 \theta$

Многие слагаемые в этом уравнении взаимно уничтожаются, и после несложных преобразований имеем:

$r(\theta) = \cfrac{2R_1 R_2}{R_1 + R_2 + (R_2 - R_1)\cos \theta}$

Чтобы найти скорость планеты, мы вычисляем производную по времени:

$\mathbf{v}(\theta) = \cfrac{\mathrm{d}\mathbf{r}(\theta)}{\mathrm{d}t} = \cfrac{\mathrm{d}\mathbf{r}(\theta)}{\mathrm{d}\theta} \cfrac{\mathrm{d}\theta}{\mathrm{d}t}$

Угловую скорость dθ/dt можно выразить через момент импульса и расстояния до Солнца:

$\cfrac{\mathrm{d}\theta}{\mathrm{d}t} = \cfrac{L}{m r^2(\theta)}$

Согласно правилу дифференцирования произведения, производная радиус-вектора по θ равна:

$\cfrac{\mathrm{d}\mathbf{r}(\theta)}{\mathrm{d}\theta} = \cfrac{\mathrm{d}r(\theta)}{\mathrm{d}\theta} (\cos \theta, \sin \theta) + r(\theta) (-\sin \theta, \cos \theta)$

$\cfrac{\mathrm{d}r(\theta)}{\mathrm{d}\theta} = \cfrac{2 R_1 R_2 (R_2 - R_1) \sin \theta}{(R_1 + R_2 + (R_2 - R_1) \cos \theta)^2}$

Подставляя все в выражение вектора скорости, имеем:

$\mathbf{v}(\theta) = \cfrac{L}{2m R_1 R_2} \left[ (0, R_2 - R_1) + (R_1 + R_2) (- \sin \theta, \cos \theta) \right]$

Другими словами, концы векторов образуют окружность с центром в точке (0, L (R₂ – R₁) / (2 m R₁ R₂)) и радиусом L (R₁ + R₂) / (2 m R₁ R₂). Именно эта окружность, как мы выяснили выше, проходит через четыре исходные точки.

Орбиты равной энергии

Предположим, что планета обращается вокруг Солнца, и ее полная энергия – сумма кинетической, обусловленной скоростью движения, и потенциальной, зависящей от расстояния до Солнца, – равна E. Какие еще орбиты будут обладать той же самой энергией?

Полную энергию можно выразить через L, m, R₁ и R₂. Для начала мы представим энергию планеты в виде выражения, включаюещго в себя гравитационную постоянную G и массу Солнца M_S:

$E$ = Кинетическая энергия в перигелии + Потенциальная энергия в перигелии = $\cfrac{m v_{\mathrm{Perihelion}}^2}{2} - \cfrac{G M_S m}{R_1} = \cfrac{L^2}{2m R_1^2} - \cfrac{G M_S m}{R_1}$

Аналогичным образом мы можем вычислить энергию планеты в афелии, что в итоге даст нам:

$E = \cfrac{L^2}{2m R_2^2} - \cfrac{G M_S m}{R_2}$

Приравняв оба выражения и решив полученное уравнение относительно GM_S, мы получим:

$G M_S = \cfrac{L^2 (R_1 + R_2)}{2m^2 R_1 R_2}$

Подставляя этот результат в любую из двух формул, имеем:

$E = -\cfrac{L^2}{2m R_1 R_2}$

Рассчитав скорость планеты, движущейся параллельно орбитальной оси, мы увидим, что она зависит только от полной энергии E массы планеты m:

$v_{\mathrm{parallel}} = \cfrac{L}{m \sqrt{R_1 R_2}} = \sqrt{-\cfrac{2E}{m}}$

Один из способов получить орбиты с той же самой энергией – воспользоваться поворотом, который оставляет неизменным Солнце, но меняет расположение планеты. Для этой цели подойдет любой трехмерный поворот – в итоге мы получим новую орбитe той же формы, но иначе ориентированную в пространстве.

Найти альтернативные орбиты с той же самой энергией можно и иначе. Если мы схватим планету в любой из точек, где ее скорость параллельна оси, а затем передвинем ее вдоль дуги окружности с центром в Солнце, то положение планеты изменится, в то время как расстояние до Солнца останется прежним. Но вместо того, чтобы аналогичным образом (как это имело бы место при повороте орбиты целиком) повернуть вектор скорости, мы оставляем его без изменений, сохраняя как направление, так и абсолютную величину.

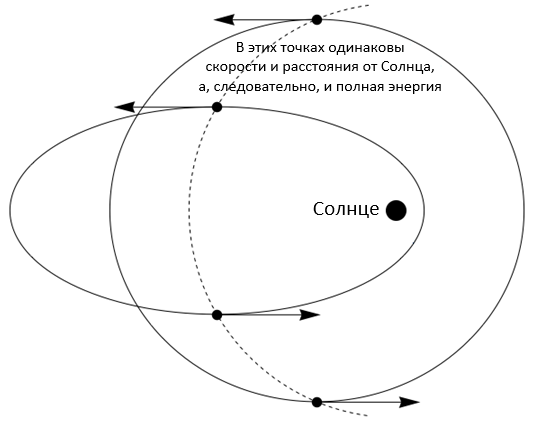
Поскольку мы не изменили расстояние планеты от Солнца, ее потенциальная энергия осталась такой же, как раньше; то же самое касается и кинетической энергии, так как при таком преобразовании планета сохраняет свою скорость. Более того, поскольку при заданной массе скорость планеты при движении параллельно орбитальной оси зависит только от ее полной энергии, она будет находиться в этом же состоянии и относительно своей новой орбиты, а значит новая орбитальная ось должна быть параллельна старой.

Орбиты, порождаемые этой процедурой, (а) обладают одной и той же энергией, (b) имеют общую ось и (с) характеризуются одной и той же парой антипараллельных скоростей, соответствующих точкам, в которых планета движется параллельно орбитальной оси. Это означает, что именно в этих точках будут пересекаться все окружности, описываемые концами векторов скорости.

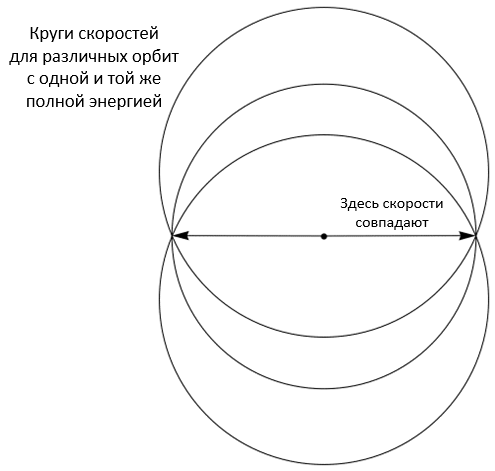
Другой способ получить то же самое семейство окружностей – применить стереографическую проекцию к сфере подходящего размера, кот\орая касается плоскости круга скоростей. Для этого мы проводим прямые через “северный полюс” и точки, лежащие на больших окружностях, проходящих через оба конца горизонтального диаметра сферы, продолжая их до пересечения с касстельной плоскостью. В результате каждая из таких больших окружностей отображается на некотоую окружность скоростей.

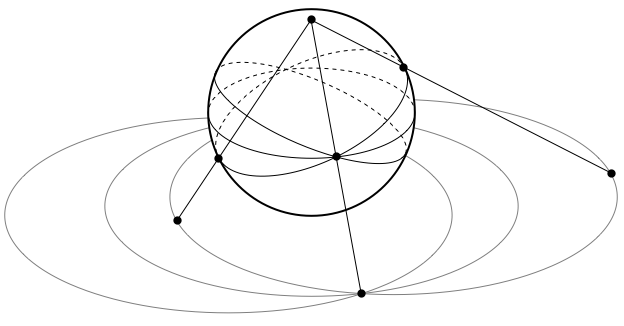
Радиус s такой сферы должен составлять половину скорости планеты в момент движения параллельно орбитальной оси:

$s = \cfrac{1}{2} \sqrt{-\cfrac{2E}{m}}$

Тем самым мы гарантируем, что в проекции расстояние от начала координат до точки, в которой прямая, проходящая через северный полюс, пересекает плоскость, будет вдвое больше – что в итоге даст нам пару точек, в которых пересекаются границы всех подходящих нам кругов скоростей.

Мы введем систему координат таким образом, чтобы плоскость круга скоростей имела вид z=–s, центр сферы находился в точке (0, 0, 0), а ее северный полюс – в точке (0, 0, s). Ось x будет соответствовать главной оси нашей эллиптической орбиты. Произвольная точка (x, y, z) трехмерного пространства над плоскостью скоростей в проекции на эту плоскость преобразуется в:

$S(x, y, z) = \cfrac{2s}{s - z} (x, y)$ ,

где мы опускаем в проекции постоянную z-координату, равную –s, и интерпретируем S как отображение на двумерную плоскость.

Экватор сферы будет отображаться в круг скоростей, соответствующий круговой орбите с центром в начале координат и радиусом √(–2 E/m). Если мы повернем экватор относительно оси x на некоторый угол α, то его произвольная точка будет иметь вид (s cos θ, s cos α sin θ, s sin α sin θ). Проекция этой точки выражается формулой:

$S(s \cos \theta, s \cos \alpha \sin \theta, s \sin \alpha \sin \theta) = \cfrac{2s}{1 - \sin \alpha \sin \theta} (\cos \theta, \cos \alpha \sin \theta)$

В совокупности проекции всех таких точек будут лежать на окружности с центром (0, 2 s tg α) и радиусом 2 s sec α.

Теперь нам будет удобно ввести орбитальную “константу взаимодействия”, которая включает в себя гравитационную постоянную G, массу Солнца M_S и массу планеты m:

$k = G M_S m = \cfrac{L^2 (R_1 + R_2)}{2m R_1 R_2}$

Радиус круга скоростей, который мы ранее представили в виде L (R₁ + R₂) / (2 m R₁ R₂), можно выразить через константу взаимодействия и момент импульса:

Радиус = $\cfrac{k}{L}$

Следовательно:

$2s \sec \alpha = \cfrac{k}{L}$

$L \sqrt{-\cfrac{2E}{m}} = k \cos \alpha$

Особый случай α=π/2, при котором круг скоростей становится бесконечным большим, соответствует орбите с нулевым моментом импульса – при этом планета падает на Солнце, а поскольку в нашей идеализированной модели Солнце представляет собой точечную массу, скорость планеты возрастает до бесконечности.

Пока что наши рассуждения по большей части опирались на то, что орбита планеты занимает некую фиксированную плоскость, хотя на самом деле плоскость орбиты, разумеется, может быть совершенно любой. Поэтому в более общем случае вместо проецирования сферы в трехмерном пространстве на плоскость нам потреубется проекция 3-сферы (трехмерной поверхности четырехмерного шара) в трехмерное пространство. Любой большой круг такой 3-сферы по-прежнему проецируется на круг скоростей, однако сами круги скоростей теперь могут иметь произвольную ориентацию в трехмерном пространстве. А любой четырехмерный поворот 3-сферы радиуса s переводит один большой круг, соответствующий некоторой орбите с энергией E, в другой большой круг, орбита которого обладает той же самой энергией.

Квантовый спин в трех измерениях

Рассмотрим поворот трехмерного тела на некоторый угол θ вокруг оси. Смену координат в любой точке тела можно описать при помощи матрицы, которую мы обозначим R_xy(θ):

$R_{xy}(\theta) = \left(\begin{array}{ccc}\cos \theta &-\sin \theta&0\\ \sin \theta&\cos \theta&0\\ 0&0&1\end{array}\right)$

Чтобы получить новые координаты точки повернутого тела, мы польуземся операцией матричного умножения:

$\mathbf{r}' = R_{xy}(\theta) \mathbf{r}$ ,

где r=(x, y, z) – старые, а r‘=(x‘, y‘, z‘) – новые координаты точки. Например, координатные оси при таком повороте принимают вид:

$R_{xy}(\theta)(1, 0, 0) = (\cos \theta, \sin \theta, 0)$

$R_{xy}(\theta)(0, 1, 0) = (-\sin \theta, \cos \theta, 0)$

$R_{xy}(\theta)(0, 0, 1) = (0, 0, 1)$

Почему мы обозначаем эту матрицу R_xy(θ), а не R_z(θ), если учесть, что она описывает поворот относительно оси z? При повороте вокруг оси z координата z остается неизменной, поэтому мы делаем выбор в пользу обозначения, в котором явно указаны изменяющиеся переменные x и y. Это правило легко обобщается на случай пространств, содержащих более трех измерений, в которых простейшие повороты затрагивают лишь заданную пару координат, в то время как все остальные координаты (сколько бы их ни было) сохраняют свои значения.

Аналогичные матрицы можно построить для поворотов вокруг осей x и y, а также поворотов относительно любой другой оси. Суммарный результат двух и более поворотов можно найти, перемножив соответствующие им матрицы. Например, если мы сначала повернем тело на угол θ вокруг оси z, а затем на угол φ вокруг оси x, то полное преобразование будет описываться умножением исходных координат на матрицу:

$T = R_{yz}(\varphi) R_{xy}(\theta)$

Матрица, описывающая первый поворот, стоит справа, поскольку при вычислении результатов поворота исходные координаты записываются в позиции правого сомножителя. Умножение матриц не обладает свойством коммутативности: результат зависит от порядка сомножителей, поэтому R_yz(φ) R_xy(θ) не эквивалентно R_xy(θ) R_yz(φ). Это факт, разумеется, отражает геометрические свойства поворотов: вращение тела вокруг двух различных осей дает разные результаты в зависимости от того, какая ось выбрана первой.

Оказывается, что для описания этой некоммутативности существует весьма эффективный способ, в основе которого лежит замена матриц поворота на матрицы, которые получаются, если мы вначале описываем поворот на угол θ, дифференцируем полученную матрицу по θ, а затем полагаем θ равным нулю. Например:

$J_{xy} = \cfrac{\mathrm{d}R_{xy}(\theta)}{\mathrm{d}\theta} \bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}-\sin \theta &-\cos \theta&0\\ \cos \theta&-\sin \theta&0\\ 0&0&1\end{array}\right)\bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}0 &-1&0\\ 1&0&0\\ 0&0&0\end{array}\right)$

Физически эта величина описывает так называемую матрицу угловых скоростей, то есть матрицу, умножая которую на координаты точек вращающегося тела, мы получаем их скорость при повороте вокруг заданной оси. В этом случае мы бы подставили θ=ωt и продифференцировали результат по t, но это бы лишь добавило к матрице множитель ω. Аналогично:

$J_{yz} = \cfrac{\mathrm{d}R_{yz}(\theta)}{\mathrm{d}\theta} \bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}0 & 0 &0\\ 0 &-\sin \theta& - \cos \theta\\ 0 & \cos \theta & -\sin \theta\end{array}\right)\bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}0 & 0 &0\\ 0 & 0 & -1\\ 0 & 1 & 0\end{array}\right)$

$J_{zx} = \cfrac{\mathrm{d}R_{zx}(\theta)}{\mathrm{d}\theta} \bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}-\sin \theta & 0 & \cos \theta\\ 0 & 0 &0\\ - \cos \theta & 0 & -\sin \theta\end{array}\right)\bigg\rvert_{\theta = 0} = \left(\begin{array}{ccc}0 & 0 & 1\\ 0 & 0 & 0\\ -1 & 0 & 0\end{array}\right)$

Все эти матрицы антисимметричны: отражение их элементов относительно главной диагонали, при котором столбы становятся строками и наоборот, дает в результате исходную матрицу с обратным знаком. Множество всех антисимметричных матриц размера 3 × 3 можно представить в виде трехмерного векторного пространства; оказывается, что поворот вокруг произвольной оси всегда описывается антисимметричной матрицей, которую можно представить в виде линейной комбинации из трех матриц J. Если ось вращения задана вектором a=(a_x, a_y, a_z), то соответствующая матрица угловых скоростей имеет вид:

$J_{\mathbf{a}} = a_x J_{yz} + a_y J_{zx} + a_z J_{xy}$

Матрицы J не коммутируют друг с другом, однако уловить характер их некоммутативности проще, чем в случае матриц поворота. Для начала мы введем для произвольной пары матриц понятие коммутатора:

$[A, B] = AB - BA$

Коммутатор, очевидно, равен нулю, если матрицы коммутируют, то есть A B = B A. В случае J-матриц, соответствующих парам координат, коммутаторы принимают на удивление простой вид:

$\left[ J_{yz}, J_{zx} \right] = J_{xy}$

$\left[ J_{zx}, J_{xy} \right] = J_{yz}$

$\left[ J_{xy}, J_{yz} \right] = J_{zx}$

Эти уравнения охватывают все возможные варианты, поскольку при перестановке матриц коммутатор меняет знак ([B, A] = –[A, B]) и любая матрица коммутирует сама с собой ([A, A] = 0).

Теперь, для того, чтобы провести аналогию с квантовой механикой, рассмотрим три оператора на функциях трех координат – скажем, f(x, y, z):

$L_{xy} f = -i\hbar (x \partial_y f - y \partial_x f)$

$L_{yz} f = -i\hbar (y \partial_z f - z \partial_y f)$

$L_{zx} f = -i\hbar (z \partial_x f - x \partial_z f)$ ,

где i – квадратный корень из минус единицы, а ℏ – “приведенная постоянная Планка”, ℏ=h/(2π). Мы можем вычислить коммутаторы этих операторов, заменяя матричное умножение последовательным применением операторов к произвольной функции f(x, y, z):

$\left[ L_{yz}, L_{zx} \right] f = L_{yz} (L_{zx} f) - L_{zx} (L_{yz} f)$

Воспользовавшись определением этих операторов, имеем:

$\left[ L_{yz}, L_{zx} \right] = i \hbar L_{xy}$

$\left[ L_{zx}, L_{xy} \right] = i \hbar L_{yz}$

$\left[ L_{xy}, L_{yz} \right] = i \hbar L_{zx}$

Как нетрудно видеть, эта закономерность довольно сильно напоминает поведение коммутаторов J-матриц. Это сходство можно выразить более формальным языком, сказав, что у нас имеется представление алгебры трехмерных поворотов (векторное пространство матриц J, также известное как so(3)) в векторном пространстве функций трехмерного пространства, заданное отображением каждой из матриц J на соответствующий оператор L. Если мы положим:

$\mathrm{d}\rho(J_{\alpha \beta}) = \cfrac{L_{\alpha \beta}}{i\hbar}$ ,

(где αβ обозначает произвольную пару координат), то далее сможем расширить dρ на любую линейную комбинацию координатных J-матриц, потребовав, чтобы dρ была линейной функцией. В этом случае:

$\left[ \mathrm{d} \rho(J_{\mathbf{a}}), \mathtm{d} \rho(J_{\mathbf{b}}) \right] = \mathrm{d} \rho\left( \left[ J_{\mathbf{a}}, J_{\mathbf{b}} \right] \right)$

Другими словами, под представлением мы понимаем функцию наподобие dρ, которая “сохраняет” коммутатор – в том смысле, что мы получаем один и тот же результат вне зависимости от того, действуем ли мы этой функцией на коммутатор исходных матриц, либо вначале применяем ее к матрицам, а затем вычисляем коммутатор.

Какой смысл несут операторы L? В квантовой механике проекция импульса частицы на заданное направление определяется производной ее волновой функции ψ(x, y, z) по этому направлению, с дополнительным множителем –iℏ. Например, импульс в направлении оси x имеет вид:

$p_x \psi(x, y, z) = -i\hbar \partial_x \psi(x, y, z)$

Если волновая функция описывает частицу, которая характеризуется определенным значение некоторой величины – например, импульса, – то соответствующий оператор просто умножает волну на это значение. Поэтому, если волновая функция, к примеру, имеет вид ψ(x, y, z)=exp(i P x / ℏ), то:

$p_x \psi(x, y, z) = -i\hbar \partial_x \exp\left(\cfrac{iPx}{\hbar}\right) = P \exp\left(\cfrac{iPx}{\hbar}\right) = P \psi(x, y, z)$

Другими словами, данная волновая функция характеризуется определенным значением x-проекции импульса – равным P. В этом случае мы можем сказать, что функция ψ является собственной функцией оператора импульса, с собственным значением P.

Вектор момента импульса, L, в случае классической частицы определяется векторным произведением радиус-вектора частицы на ее импульс:

$\mathbf{L} = \mathbf{r} \times \mathbf{p}$

Если мы раскроем векторное произведение для каждой из координат, а затем преобразуем компоненты импульса в их квантовомеханические аналоги, то получим:

$L_x = y p_z - z p_y \rightarrow -i\hbar (y \partial_z - z \partial_y) = L_{yz}$

$L_y = z p_x - x p_z \rightarrow -i\hbar (z \partial_x - x \partial_z) = L_{zx}$

$L_z = x p_y - y p_x \rightarrow -i\hbar (x \partial_y - y \partial_x) = L_{xy}$

Таким образом, операторы L представляют собой квантовомеханические аналоги компонент вектора момента импульса. Сходство между коммутаторами этих операторов и матриц J не так уж удивительно, если учесть, что матрицы J по сути являются инструментом для вычисления угловых скоростей, а момент импульса изолированной частицы есть не что иное, как произведение ее момента инерции на угловую скорость¹.

Мы можем определить оператор, соответствующий квадрату модуля момента импульса:

$L^2 f = L_{yz} (L_{yz}f) + L_{zx} (L_{zx}f) + L_{xy} (L_{xy}f)$

Оператор L² коммутирует со всеми компонентами момента импульса.

Теперь нашей целью будет поиск различных векторных пространств волновых функций, инвариантных относительно поворотов системы координат: другими словами, если ψ(r) – функция в векторном пространстве, а R – некоторый поворот, то в этом же векторном пространстве должна находиться и функция ψ_R(r) = ψ(R r). [Заметим, что инвариантным является векторное пространство в целом. Мы не утверждаем, что повороты сохраняют отдельные функции этого пространства.] С физической точки зрения поворот замкнутой квантовой системы (или переход к ее описанию в новой системе координат, повернутой относительно старой) приводит к изменению ее волновой функции, и нам бы хотелось знать, какие векторные пространства содержат все волновые функции, которые можно получить, поворачивая произвольную из них.

Примером пространства функций, инвариантных относительно вращений системы координат, может служить множество всех однородных многочленов заданной степени, зависящих от переменных x, y и z. Многочлен называется однородным, если каждое из слагаемых характеризуется одной и той же суммой степеней, взятых по всем переменным. Такая сумма называется степенью многочлена. Например:

$f(x, y, z) = 7 x^2 yz + 3xy z^2$

представляет собой однородный многочлен четвертой степени. Как нетрудно видеть, при любом линейном преобразовании координат – то есть замене каждой из координат на некоторую линейную комбинацию исходных переменных – мы снова получим однородный многочлен той же степени. Поскольку поворот является линейным преобразованием, пространство однородных многочленов любой фиксированной степени будет инвариантным относительно вращений.

В качестве дополнительного упрощения мы ограничимся поиском функциональных пространств, которые помимо инвариантности относительно вращений, не содержат в себе других инвариантных пространств. Такие пространства мы будем называть неприводимыми. Оказывается, что пространство однородных многочленов заданной степени действительно содержит в себе инвариантное подпространство – а именно, пространство многочленов, удовлетворяющих уравнению Лапласа:

$\nabla^2 f = 0$

где оператор Лапласа ∇² в трехмерном пространстве определяется как сумма вторых производных по трем координатам:

$\nabla^2 f = \partial_{xx} f + \partial_{yy} f + \partial_{zz} f$

Чтобы понять, почему множество решений уравнения Лапласа инвариантно относительно вращений, нужно просто перейти в новую систему координат, повернутую относительно исходной. Если мы обозначим исходные координаты как x^j, где j=1,2,3, то оператор Лапласа можно представить в виде:

$\nabla^2 f = \sum_j \partial_{x^j, x^j} f$

Наши новые координаты ξⁱ, в повернутой системе, будут связаны со старыми соотношением:

$\xi^i = \sum_j R_{ij} x^j$

где R_ij – координаты матрицы поворота. Воспользовавшись правилом дифференцирования сложной функции, имеем:

$\begin{split} & \nabla^2 f = \sum_j \partial_{x^j, x^j} f = \\ & = \sum_j \sum_\alpha \sum_\beta (\partial_{x^j} \xi^\alpha) (\partial_{x^j} \xi^\beta) \partial_{\xi^\alpha, \xi^\beta} f = \\ & = \sum_\alpha \sum_\beta \left( \sum_j R_{\alpha j} R_{\beta j} \right) \partial_{\xi^\alpha, \xi^\beta} f = \\ & = \sum_\alpha \sum_\beta \delta_{\alpha \beta} \partial_{\xi^\alpha, \xi^\beta} f = \\ & = \sum_\alpha \partial_{\xi^\alpha, \xi^\alpha} f \end{split}$

что совпадает с выражением лапласиана в новых координатах. Символ δ_αβ, которым мы воспользовались на шаге:

$\sum_j R_{\alpha j} R_{\beta j} = \delta_{\alpha \beta}$

называется символом Кронекера: он равен 1, если α равно β, и 0 – в противном случае. Этот шаг эквивалентен утверждению, что произведение матрицы поворота на результат ее транспонирования дает единичную матрицу, или, выражаясь другими словами, что скалярное произведение двух одинаковых строк матрицы всегда равно единице, а двух различных – нулю. Нетрудно показать, что это должно быть верно для столбцов исходной матрицы, поскольку столбцы – это векторы, в которые координатные оси переходят в процессе поворота. Утверждение о столбцах соответствует матричному уравнению R^TR=I, в то время как утверждение о строках – уравнению RR^T=I. Но у любой обратимой матрицы есть только одна обратная, причем умножение на нее слева дает тот же результат, что и справа. Отсюда следует, что матрица R^T обратна R, и, следовательно, утверждение о строках также верно.

Шаровая функция – это решение уравнения Лапласа, представляющее собой однородный многочлен в декартовых координатах. Шаровую функцию степени λ мы будем обозначать Z_{λ, σ}(x, y, z), где λ – неотрицательное целое, а второй индекс σ обозначает некоторый, пока что не определенный способ пометки отдельных многочленов. При любом фиксированном значении λ, пространство, образуемое линейными комбинациями этих функций, инвариантно относительно поворотов и является неприводимым, то есть не содержит инвариантных подпространств.

Сферической (не путать с шаровой) функцией, соответствующей единичному вектору u, мы будем называть:

$Y_{\lambda, \sigma}(\mathbf{u}) = Z_{\lambda, \sigma}(\mathbf{u})$

Таким образом, Y_{λ, σ} определена только на единичной сфере S², в пределах которой она совпадает с Z_{λ, σ}. Поскольку шаровые функции являются однородными многочленами, то при изменении масштаба аргумента они умножаются на коэффициент пропорциональности в степени λ и, следовательно:

$Z_{\lambda, \sigma}(\mathbf{r}) = r^\lambda Z_{\lambda, \sigma}(\mathbf{r}/r) = r^\lambda Y_{\lambda, \sigma}(\mathbf{r}/r)$

Если мы применим оператор L² к функции Z_{λ, σ} и воспользуемся тем фактом, что Z_{λ, σ} является решением уравнения Лапласа, то получим в результате:

$L^2 Z_{\lambda, \sigma}(\mathbf{r}) = \hbar^2 \lambda (\lambda + 1) Z_{\lambda, \sigma}(\mathbf{r}) - \hbar^2 r^2 \nabla^2 Z_{\lambda, \sigma}(\mathbf{r}) = \hbar^2 \lambda (\lambda + 1) Z_{\lambda, \sigma}(\mathbf{r})$

Другими словами, все шаровые функции степени λ являются собственными функциями оператора, выражающего квадрат момента импульса, с соответствующим собственным значением ℏ² λ(λ+1). То же самое будет верно и для любой линейной комбинации Z_{λ, σ} с одним и тем же λ. Таким образом, каждому из таких инвариантных функциональных пространств соответствует отдельная величина, описывающая квадрат момента импульса.

Функциональное пространство, образованное линейными комбинациями функций Z_{λ, σ}, мы будем называть λ-спинорным представлением алгебры вращений. Чтобы определить его размерность, мы для начала обратим внимание на то, что в случае двух переменных число возможных одночленов степени λ, как нетрудно видеть, равно λ+1, поскольку выбор степени для первой переменной – в диапазоне от от 0 до λ – полностью определяет и степень второй. В случае трех переменных мы можем взять любой одночлен от двух переменных, степень которого варьируется от 0 до λ и умножить его на третью переменную, возведенную в недостающую степень, что в общей сложности дает нам:

$1 + 2 + \dots + (\lambda + 1) = \cfrac{(\lambda + 1)(\lambda + 2)}{2}$

Оператор Лапласа понижает степень однородного многочлена на два, поэтому приравнивая его к нулю, мы накладываем ½λ(λ–1) ограничений. Размерность нашего пространства будет определяться разностью этих величин, которая равна 2λ+1. Таким образом, λ-спинорное представление имеет размерность 2λ+1.

Чтобы придать этому выводу физический смысл, мы можем ввести в пространстве базис, каждый элемент которого характеризуется отличным от других собственным значением одного из операторов L – скажем, L_xy, измеряющего проекцию момента импульса на ось z. Если мы положим по определению:

$Z_{\lambda, \lambda}(x, y, z) = (x + iy)^\lambda$

то, очевидно, получим однородный многочлен степени λ. Непосредственными расчетами можно убедиться в том, что:

$\nabla^2 Z_{\lambda, \lambda} = 0$

$L_{xy} Z_{\lambda, \lambda} = \lambda \hbar Z_{\lambda, \lambda}$

Итак, мы нашли в λ-спинорном представлении одну из функций, для которых проекция момента импульса на ось z в точности равна λ (если измерять ее в квантовых спиновых единицах, ℏ). Аналогичным образом можно определить функцию, для которой z-проекция момента импульса имеет противоположное значение:

$Z_{\lambda, -\lambda}(x, y, z) = (x - iy)^\lambda$

$\nabla^2 Z_{\lambda, -\lambda} = 0$

$L_{xy} Z_{\lambda, -\lambda} = -\lambda \hbar Z_{\lambda, -\lambda}$

Предположим теперь, что у нас есть функция Z_λ,_m, которая является собственной функцией L_xy, и соответствующее ей собственное значение равно mℏ. Далее мы воспользуемся коммутаторами L-операторов:

$\left[ L_{xy}, L_{yz} \right] = i \hbar L_{zx}$

$L_{xy} L_{yz} = i \hbar L_{zx} + L_{yz} L_{xy}$

$\left[ L_{zx}, L_{xy} \right] = i \hbar L_{yz}$

$-L_{xy} L_{zx} = i \hbar L_{yz} - L_{zx} L_{xy}$

Теперь мы определим «оператор понижения спина»:

$L_{-} = L_{yz} - i L_{zx}$

Если мы применим этот оператор к Z_λ,_m, известной нам собственной функции L_xy с собственным значением mℏ, то получим:

$\begin{split} & L_{xy} \left(L_{-} Z_{\lambda, m}\right) = \\ & = L_{xy}\left( L_{yz} - i L_{zx} \right) Z_{\lambda, m} = \\ & = \left( L_{xy} L_{yz} - i L_{xy} L_{zx} \right) Z_{\lambda, m} = \\ & = \left( i\hbar L_{zx} + L_{yz} L_{xy} + i\left(i\hbar L_{yz} - L_{zx} L_{xy} \right) \right) Z_{\lambda, m} = \\ & = \left( i\hbar L_{zx} + m\hbar L_{yz} + i\left(i\hbar L_{yz} - m\hbar L_{zx} \right) \right) Z_{\lambda, m} = \\ & = (m - 1) \hbar \left( L_{yz} - i L_{zx} \right) Z_{\lambda, m} = \\ & = (m - 1)\hbar (L_{-}Z_{\lambda, m}) \end{split}$

Таким образом, L_– порождает новую собственную функцию L_xy, собственное значение которой на единицу меньше исходного. Этот процесс, однако же, не может продолжаться до бесконечности. Применив оператор понижения спина к Z_{λ, –λ}, имеем:

$\begin{split} & L_{-} Z_{\lambda, -\lambda} = \\ & = \left( L_{yz} - iL_{zx} \right) (x - iy)^\lambda = \\ & = -i\hbar \left( y\partial_z - z \partial_y - iz \partial_x + ix \partial_z \right) (x - iy)^\lambda = \\ & = i\hbar z (\partial_y + i \partial_x) (x - iy)^\lambda = \\ & = 0 \end{split}$

Итак, мы получаем базис {Z_{λ, –λ}, Z_{λ, –λ+1}, …, Z_{λ, λ–1}, Z_{λ, λ}} λ-спинорного представления, содержащий ровно 2λ+1 элементов, каждый из которых является собственной функцией L_xy и характеризуется собственным значением, выраженным в целочисленных единицах из диапазона от –λ до λ.

Оказывается, что все неприводимые представления алгебры вращений имеют точно такую же структуру, что и функциональные пространства, которые мы назвали λ-спинорными представлениями: все их можно охарактеризовать числом λ, связанным с их размерностью 2λ+1, и базисом собственных векторов одной из компонент момента импульса, причем соответствующие им собственные значения будут пропорциональны целому числу, варьирующемуся от –λ до λ. Это утверждение мы, однако же, оставим без доказательства. Единственный аспект, который невозможно продемонстрировать на наших примерах волновых функций – это допустимость полуцелых значений. Так, векторное пространство, описывающее собственный спин электрона, является ½-спинорным представлением: его размерность равна двум, а z-компонента спина может принимать одно из значений –½ℏ или ½ℏ.

Квантовый спин в четырех измерениях

Если мы расширим идеи предыдущего параграфа на четырехмерное пространство (добавив к исходным координатам x, y и z четвертую w), то сможем аналогичным образом ввести матрицы поворота так, чтобы они учитывали три новых пары координат. Взяв их производные, мы получим три новые матрицы J: J_xw, J_yw, J_zw. Алгебру четырехмерных поворотов можно вкратце охарактеризовать следующим утверждением: для любых попарно различных i, j, k:

$\left[ J_{ij}, J_{kj} \right] = J_{ik}$

Если не считать перестановок в этом базовом тождестве, все остальные коммутаторы равны нулю. Это довольно просто, но оказывается, что еще большего упрощения можно добиться, выбрав другой набор матриц.

$A_x = \cfrac{J_{yz} + J_{xw}}{2} = \left(\begin{array}{cccc}0 & 1/2 & 0 & 0\\ -1/2 & 0 & 0 & 0\\ 0 & 0 & 0 & -1/2\\ 0 & 0 & 1/2 & 0 \end{array}\right)$

$A_y = \cfrac{J_{zx} + J_{yw}}{2} = \left(\begin{array}{cccc}0 & 0 & 1/2 & 0\\ 0 & 0 & 0 & 1/2\\ -1/2 & 0 & 0 & 0\\ 0 & -1/2 & 0 & 0 \end{array}\right)$

$A_z = \cfrac{J_{xy} + J_{zw}}{2} = \left(\begin{array}{cccc}0 & 0 & 0 & 1/2\\ 0 & 0 & -1/2 & 0\\ 0 & 1/2 & 0 & 0\\ -1/2 & 0 & 0 & 0 \end{array}\right)$

$B_x = \cfrac{J_{yz} - J_{xw}}{2} = \left(\begin{array}{cccc}0 & -1/2 & 0 & 0\\ 1/2 & 0 & 0 & 0\\ 0 & 0 & 0 & -1/2\\ 0 & 0 & 1/2 & 0 \end{array}\right)$

$B_y = \cfrac{J_{zx} - J_{yw}}{2} = \left(\begin{array}{cccc}0 & 0 & -1/2 & 0\\ 0 & 0 & 0 & 1/2\\ 1/2 & 0 & 0 & 0\\ 0 & -1/2 & 0 & 0 \end{array}\right)$

$B_z = \cfrac{J_{xy} - J_{zw}}{2} = \left(\begin{array}{cccc}0 & 0 & 0 & -1/2\\ 0 & 0 & -1/2 & 0\\ 0 & 1/2 & 0 & 0\\ 1/2 & 0 & 0 & 0 \end{array}\right)$

Коммутаторы этих матриц имеют вид:

$[A_x, A_y] = A_z$ , и далее согласно циклическим перестановкам;
$[B_x, B_y] = B_z$ , и далее согласно циклическим перестановкам;
$[A_i, B_j] = 0$ , для любых i и j.

Другими словами, отдельные «подалгебры», образованные матрицами A и B, имеют ту же самую структуру, что и алгебра трехмерных поворотов so(3), а все коммутаторы между алгебрами равны нулю.

В общем случае мы, таким образом, ожидаем получить неприводимое представление алгебры четырехмерных поворотов so(4), выбрав два числа λ_A и λ_B и комбинируя λ_A– и λ_B-спинорные представления алгебры трехмерных поворотов so(3). Так как мы можем ввести операторы понижения спина, независимо действующие на собственные значения A_z и B_z, то эти собственные значения будут независимо варьироваться в рамках соответствующих интервалов, что даст нам в общей сложности (2λ_A+1)(2λ_B+1) различных векторов в качестве базиса для пространства в целом.

Однако, если мы имеем дело с функциями в четырехмерном пространстве, расширение операторов L на все шесть пар координат приведет к тому, что эти представления всегда будут удовлетворять условию λ_A=λ_B. Причина состоит в том, что эти функции описывают квантовую механику одной частицы, и хотя четырехмерная угловая скорость может в общем случае включать произвольную линейную комбинацию из шести матриц J, угловая скорость точечной частицы всегда предполагает движение в пределах одной плоскости – а именно, плоскости, образованной всевозможными линейными комбинациями радиус-вектора частицы и ее вектора скорости.

Предположим, что угловая скорость представлена в виде линейной комбинации матриц A и B:

$J = a_x A_x + a_y A_y + a_z A_z + b_x B_x + b_y B_y + b_z B_z$

Поскольку движение ограничено одной плоскостью, мы всегда можем выбрать координаты так, чтобы:

$J = \omega J_{xy} = \omega A_z + \omega B_z$

$a_x = a_y = b_x = b_y = 0$

$a_z = b_z = \omega$

$a_x^2 + a_y^2 + a_z^2 = b_x^2 + b_y^2 + b_z^2$

Точные значения a_x, b_x и т. д. зависят от выбора координат, но можно показать, что последнее выражение, устанавливающее равенство между суммами квадратов для коэффициентов a и b, остается верным в любой системе координат. Таким образом, при любом простом повороте (т. е. повороте в пределах одной плоскости), тройки коэффициентов, соответствующих матрицам A и B, характеризуются одним и тем же квадратом модуля.

Для доказательства квантовомеханического аналога этого утверждения, мы в целях упрощения обозначений введем ряд трехмерных векторов, составленных из операторов:

$\mathbf{L} = (L_{yz}, L_{zx}, L_{xy})$

$\mathbf{M} = (L_{xw}, L_{yw}, L_{zw})$

$\mathbf{A} = \cfrac{1}{2} (\mathbf{L} + \mathbf{M})$

$\mathbf{B} = \cfrac{1}{2} (\mathbf{L} - \mathbf{M})$

В данном случае мы используем для обозначения сумм и разностей, построенных из операторов L, те же самые символы A и B, которыми мы обозначили матрицы, построенные из сумм и разностей матриц J. Мы можем определить квадрат момента импульса для пары спинов:

$A^2 = \mathbf{A} \cdot \mathbf{A} = \cfrac{1}{4} (\mathbf{L} \cdot \mathbf{L} + \mathbf{L} \cdot \mathbf{M} + \mathbf{M} \cdot \mathbf{L} + \mathbf{M} \cdot \mathbf{M})$

$B^2 = \mathbf{B} \cdot \mathbf{B} = \cfrac{1}{4} (\mathbf{L} \cdot \mathbf{L} - \mathbf{L} \cdot \mathbf{M} - \mathbf{M} \cdot \mathbf{L} + \mathbf{M} \cdot \mathbf{M})$

$A^2 - B^2 = \cfrac{1}{2} (\mathbf{L} \cdot \mathbf{M} + \mathbf{M} \cdot \mathbf{L})$

$A^2 + B^2 = \cfrac{1}{2} (L^2 + M^2)$

Теперь, воспользовавшись определением операторов L, мы получим, что:

$\begin{split} & (\mathbf{L} \cdot \mathbf{M}) f = \\ & = -\hbar^2 ( (y \partial_z - z \partial_y) (x \partial_w - w \partial_x) + \\ & + (z \partial_x - x \partial_z) (y \partial_w - w \partial_y) + \\ & + (x \partial_y - y \partial_x) (z \partial_w - w \partial_z) ) f = \\ & = -\hbar^2 ( (xy \partial_{z,w} + zw \partial_{x, y} - xz \partial_{y, w} - yw \partial_{x, z}) + \\ & + (yz \partial_{x, w} + xw \partial_{y, z} - xy \partial_{z, w} - zw \partial_{x, y}) + \\ & + (xz \partial_{y, w} + yw \partial_{x, z} - yz \partial_{x, w} - xw \partial_{y, z}) ) = 0 \end{split}$

Аналогичным образом, (M · L) f = 0. Таким образом, A² = B², и λ_A=λ_B.

Шаровые функции в четырех измерениях мы определяем как однородные многочлены от четырех декартовых координат x, y, z, w, удовлетворяющие четырехмерному уравнению Лапласа. Четырехмерную сферическую функцию степени λ и сферическую функцию, которая совпадает с ней на единичной сфере, мы будем обозначать как Z_{λ, σ, μ} и Y_{λ, σ, μ} соответственно. Есть множество способов для выбора отдельных функций, но один из наиболее очевидных вариантов заключается в том, чтобы приравнять σ и μ собственным значениям A_z и B_z соответственно, варьируя каждое из них от –λ_A до λ_A.

В случае трех измерений квадрат модуля момента импульса, L², не меняется под действием поворотов, а множество собственных функций L², соответствующих заданному собственному значению, образует инвариантное пространство. В четырех измерениях матрицы угловой скорости содержат шесть независимых компонент, и любая величина, не меняющаяся при повороте системы координат, должна включать в себя их все, так как в общем случае поворот может преобразовать одну из этих компонент в другую. В используемых нами обозначениях A² + B² и L² + M² (которые отличаются только множителем ½) инвариантны относительно поворотов, а четырехмерные сферические функции являются их собственными функциями:

$\begin{split} & (A^2 + B^2) Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \\ & = \cfrac{1}{2} (L^2 + M^2) Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \\ & = \cfrac{1}{2} \left( \hbar^2 \lambda (\lambda + 2) Z_{\lambda, \sigma, \mu}(\mathbf{r}) - \hbar^2 r^2 \nabla^2 Z_{\lambda, \sigma, \mu}(\mathbf{r}) \right) = \\ & = \cfrac{1}{2} \hbar^2 \lambda (\lambda + 2) Z_{\lambda, \sigma, \mu}(\mathbf{r}) \end{split}$

В третьей строке мы воспользовались только тем, что функция Z_{λ, σ, μ}(r) является однородным многочленом степени λ, в то время как четвертая использует тот факт, что Z_λ, _σ,_μ(r) удовлетворяет уравнению Лапласа. Поскольку A² = B², то отсюда следует, что:

$A^2 Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \cfrac{1}{2} \hbar^2 \lambda (\lambda + 2) Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \hbar^2 \left( \cfrac{\lambda}{2} \right) \left( \cfrac{\lambda}{2} + 1 \right) Z_{\lambda, \sigma, \mu}(\mathbf{r})$

В λ_A-спинорном представлении алгебры трехмерных поворотов A² = ℏ²λ_A(λ_A+1), поэтому должно быть справедливо равенство λ_A = λ_B = ½λ. Размерность представления, которое нам дает шаровая функция степени λ равна:

$(2\lambda_A + 1) (2\lambda_B + 1) = (\lambda + 1)^2$

В качестве проверки мы можем вычислить ту же самую размерность, напрямую подсчитав число независимых многочленов. Применив рассуждения, аналогичные тем, что мы привели для случая трехмерных сферических функций, можно показать, что количество линейно независимых многочленов степени λ, зависящих от четырех переменных, равно (λ+3)(λ+2)(λ+1)/6. Далее, в силу того, что оператор Лапласа понижает степень однородного многочлена на два, его равенство нулю накладывает (λ+1) λ (λ–1)/6 ограничений. В итоге размерность пространства, определяемая разностью этих двух выражений, оказывается равной (λ+1)².

Чтобы привести конкретные примеры сферических функций, мы можем для начала ввести:

$Z_{\lambda, \cfrac{\lambda}{2}, \cfrac{\lambda}{2}} (x, y, z, w) = (x + iy)^\lambda$

Соответствующие этим функциям собственные значения для операторов A_z и B_z равны ½ℏλ. Теперь мы можем получить собственные функции с меньшим значением спина, воспользовавшись оператором понижения:

$A_{-} = A_x - iA_y$

$B_{-} = B_x - iB_y$

Паули^[1][2] вычислил энергетические уровни водорода, догадавшись, что квантовомеханический аналог классического вектора, известного как вектор Лапласа-Рунге-Ленца (направленного вдоль оси эллиптической планетарной орбиты) при соответствующем выборе масштаба ведет себя в точности так же, как вектор M, а значит, алгебра, образуемая вектором Лапласа-Рунге-Ленца и моментом импульса L оказалась не чем иным, как замаскированной алгеброй четырехмерных поворотов! Паули не работал с функциями на четырехмерных пространствах и получил уравнение L · M = 0 из классического соотношения между моментом импульса (перпендикулярным плоскости орбиты) и вектором Лапласа-Рунге-Ленца, лежащим в орбитальной плоскости.

Мы не станем вдаваться в детали выкладок Паули, но один из аспектов упомянутой аналогии увидеть довольно просто. Для любого эллипса справедливо соотношение между большой полуосью a, малой полуосью b и расстоянием от центра до любого из фокусов c:

$b^2 + c^2 = a^2$

Если тело движется по орбите, то фиксируя полную энергию E, мы одновременно фиксируем и величину большой полуоси a. В этом случае малая полуось b оказывается пропорциональной моменту импульса L. Длина вектора Лапласа-Рунге-Ленца, M, пропорциональна эксцентриситету орбиты, который, в свою очередь, пропорционален c. Таким образом, при соответствующем выборе единиц измерения M, инвариантность величины:

$L^2 + M^2$

для любых орбит с фиксированной полной энергией всего лишь отражает тот факт, что числа a, b и c образуют пифагорейскую тройку.

Чтобы сделать следующий шаг, предположим, что мы выбрали в трехмерном пространстве два вектора A и B, руководствуясь только одним ограничением:

$A^2 = B^2 = -\cfrac{k^2 m}{8E}$

где E – некоторое фиксированное значение полной энергии. Мы, очевидно, можем независимо вращать эти векторы, не нарушая заданного ограничения. Если мы в таком случае положим:

$\mathbf{L} = \mathbf{A} + \mathbf{B}$

$\mathbf{M} = \mathbf{A} - \mathbf{B}$ ,

то окажется, что:

$\mathbf{L} \cdot \mathbf{M} = (\mathbf{A} + \mathbf{B}) \cdot (\mathbf{A} - \mathbf{B}) = \mathbf{A} \cdot \mathbf{A} - \mathbf{B} \cdot \mathbf{B} = 0$

$L^2 + M^2 = (\mathbf{A} + \mathbf{B}) \cdot (\mathbf{A} + \mathbf{B}) + (\mathbf{A} - \mathbf{B}) \cdot (\mathbf{A} - \mathbf{B}) = 2 (A^2 + B^2) = -\cfrac{k^2 m}{2E}$

Имея гарантию ортогональности векторов L и M, мы всегда можем выбрать эллиптическую орбиту так, чтобы вектор L был перпендикулярен ее плоскости, а M – направлен от центра притяжения ко второму фокусу эллипса.

Точное соотношение между энергией, моментом импульса и полуосями эллипса можно вывести из двух полученных ранее выражений:

$E = -\cfrac{L^2}{2m R_1 R_2}$

$k = G M_S m = \cfrac{L^2 (R_1 + R_2)}{2m R_1 R_2}$

$\alpha = \cfrac{1}{2} (R_1 + R_2) = -\cfrac{k}{2E}$

$b^2 = R_1 R_2 = -\cfrac{L^2}{2Em}$

Если мы выберем единицы измерения M так, чтобы его отношение к c совпадало с отношением L к b, то окажется, что:

$c^2 = -\cfrac{M^2}{2Em}$

$b^2 + c^2 = -\cfrac{L^2 + M^2}{2Em} = \cfrac{k^2}{4E^2} = a^2$

Другими словами, зафиксировав E, мы видим, что множество орбит, обладающих той же самой полной энергией, инвариантно относительно независимых вращений двух векторов A и B, что приводит к тому же самому удвоению алгебры вращений, которое мы наблюдали в случае четырехмерных поворотов.

Если мы оставим физические векторы в стороне и сосредоточимся на геометрической стороне вопроса, то для демонстрации тех же симметрий можно воспользоваться еще более простым построением. Выберем два вектора A и B равной длины. Поместим один из фокусов эллипса в начале координат, второй – в точке A + B, а точки эллипса, в которых касательная параллельна большой оси – на концах векторов A и B. В результате такого построения всегда получится эллипс с большой полуосью |A| (в вырожденном случае при A = B это будет отрезок прямой), а все семейство эллипсов, один из фокусов которых совпадает с началом координат, а большая полуось имеет одну и ту же величину, порождается независимыми вращениями векторов A и B.

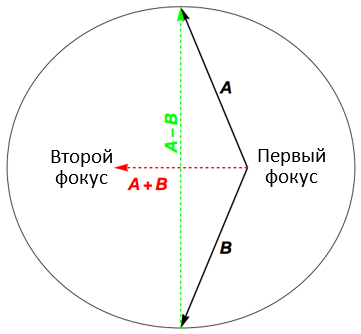
Конечно, в данном случае роль вектора B, скорее, противоположна той, которую играл B в предыдущем построении, а вектор A – B, длина которого теперь пропорциональна моменту импульса, лежит в орбитальной плоскости, а не перпендикулярен ей. Тем не менее, составляющие обеих моделей можно соотнести так, чтобы сохранилось их главное качество – наличие двух независимых трехмерных поворотов.

Фоковская проекция в импульсное пространство

В 1935 году Владимир Фок^[3] воспользовался стереографической проекцией 3-сферы в импульсное пространство (которое отличается от нашего пространства скоростей только множителем m) для анализа квантовомеханических решений, описывающих движение частицы под действием силы, квадратично убывающей с расстоянием. В квантовомеханическом случае речь, разумеется, идет об изучении не звезды с планетой, а протона и электрона. Я не знаком с исходной статьей Фока, поэтому следующим далее выкладкам я отчасти обязан Джонасу Карлссону^[4], Радославу Шмытковски^[5], а также Бэндеру и Ицыксону^[6].

Обычное уравнение Шрёдингера, описывающее частицу, движущуюся под действием обратноквадратичной силы с постоянной взаимодействия k, имеет вид:

$-\cfrac{\hbar^2}{2m} \nabla^2 \varphi(\mathbf{r}) - \left( \cfrac{k}{|\mathbf{r}|} \right) \varphi(\mathbf{r}) = E \varphi(\mathbf{r})$

Это стационарное уравнение, описывающее собственную функцию φ(r) с энергией E. В данном случае мы представили состояние частицы φ(r) в виде функции ее координат, r. При желании мы, тем не менее, можем выразить состояние частицы в виде функции ее импульса p. Эти представления по сути связаны аналогом преобразования Фурье:

$\varphi(\mathbf{r}) = \cfrac{1}{\sqrt{8 \pi^3 \hbar^3}} \int \limits_{R^3} \psi(\mathbf{p}) \exp \left( \cfrac{i\mathbf{p} \cdot \mathbf{r}}{\hbar} \right) \mathrm{d}^3 \mathbf{p}$

$\psi(\mathbf{p}) = \cfrac{1}{\sqrt{8 \pi^3 \hbar^3}} \int \limits_{R^3} \varphi(\mathbf{r}) \exp \left( -\cfrac{i\mathbf{p} \cdot \mathbf{r}}{\hbar} \right) \mathrm{d}^3 \mathbf{r}$

Чтобы получить уравнение Шрёдингера в импульсном пространстве, мы применяем к исходному уравнению преобразование Фурье. Наибольшую сложность составляет преобразование потенциальной энергии –k/|r|. В качестве первого шага мы введем для 1/r удобное интегральное представление:

$\int \limits_0^\infty \cfrac{\exp (-\alpha r^2)}{\sqrt{\alpha}} \mathrm{d} \alpha = \bigg \rvert_{\alpha = \beta/r^2} \cfrac{1}{r} \int \limits_0^\infty \cfrac{\exp(-\beta)}{\sqrt{\beta}} \mathrm{d} \beta = \cfrac{1}{r} \Gamma(\cfrac{1}{2}) = \cfrac{\sqrt{\pi}}{r}$ ,

где Γ – гамма-функция. Таким образом:

$\cfrac{1}{r} = \cfrac{1}{\sqrt{\pi}} \int \limits_0^\infty \cfrac{\exp (-\alpha r^2)}{\sqrt{\alpha}} \mathrm{d} \alpha$

Далее мы будем обозначать модуль произвольного вектора той же буквой, что и сам вектор, но без полужирного начертания: p для |p| и r для |r|. Используя интегральное представление 1/r, мы можем представить результат преобразования потенциальной энергии в виде:

$\begin{split} & V(\mathbf{p}) = \\ & = \cfrac{1}{\sqrt{8 \pi^3 \hbar^3}} \int \limits_{R^3} (-\cfrac{k}{r}) \exp \left( -\cfrac{i\mathbf{p} \cdot \mathbf{r}}{\hbar} \right) \mathrm{d}^3 \mathbf{r} = \\ & = -\cfrac{k}{\sqrt{8 \pi^4 \hbar^3}} \int \limits_0^\infty \cfrac{1}{\sqrt{\alpha}} \int \limits_{R^3} \exp \left( -\cfrac{i\mathbf{p} \cdot \mathbf{r}}{\hbar} \right) \exp (-\alpha r^2) \mathrm{d}^3 \mathbf{r} \mathrm{d} \alpha \end{split}$

Интеграл по R³ можно привести к полярным координатам на сфере, отсчитывая угол θ от направления вектора импульса p, так, чтобы p·r = p r cos θ.

$\begin{split} & \int \limits_{R^3} \exp \left( -\cfrac{i\mathbf{p} \cdot \mathbf{r}}{\hbar} \right) \exp (-\alpha r^2) \mathrm{d}^3 \mathbf{r} = \\ & = \int \limits_0^{2\pi} \int \limits_0^\infty \int \limits_0^\pi \exp \left( -\cfrac{ipr \cos \theta}{\hbar} \right) \sin \theta \mathrm{d}\theta \exp (-\alpha r^2) r^2 \mathrm{d}r \mathrm{d}\varphi = \\ & = 2\pi \int \limits_0^\infty \int \limits_0^\pi \exp \left( -\cfrac{ipr \cos \theta}{\hbar} \right) \sin \theta \mathrm{d}\theta \exp (-\alpha r^2) r^2 \mathrm{d}r \bigg \rvert_{z = \cos \theta} = \\ & = 2\pi \int \limits_0^\infty \int \limits_{-1}^1 \exp \left( -\cfrac{iprz}{\hbar} \right) \mathrm{d}z \exp (-\alpha r^2) r^2 \mathrm{d}r = \\ & = \cfrac{2 \pi \hbar i}{p} \int \limits_0^\infty \left( \exp \left( -\cfrac{ipr}{\hbar} \right) - \exp \left( \cfrac{ipr}{\hbar} \right) \right) \exp (-\alpha r^2) r^2 \mathrm{d}r = \\ & = \cfrac{\pi \hbar i}{p} \int \limits_{-\infty}^\infty \left( \exp \left( -\cfrac{ipr}{\hbar} \right) - \exp \left( \cfrac{ipr}{\hbar} \right) \right) \exp (-\alpha r^2) r^2 \mathrm{d}r \end{split}$

Сделав в первом слагаемом подстановку $r = u/\sqrt{\alpha} - ip/(2\hbar \alpha)$ , а во втором – $r = u/\sqrt{\alpha} + ip/(2\hbar \alpha)$ , имеем:

$\begin{split} & \cfrac{\pi}{2p\alpha^{3/2}} \exp \left( -\cfrac{p^2}{4 \hbar^2 \alpha} \right) \int \limits_{-\infty}^\infty \exp(-u^2) (p + 2i\hbar u \sqrt{\alpha}) \mathrm{d} u + \\ & + \cfrac{\pi}{2p\alpha^{3/2}} \exp \left( -\cfrac{p^2}{4 \hbar^2 \alpha} \right) \int \limits_{-\infty}^\infty \exp(-u^2) (p - 2i\hbar u \sqrt{\alpha}) \mathrm{d} u = \\ & = \cfrac{\pi}{\alpha^{3/2}} \exp \left( -\cfrac{p^2}{4 \hbar^2 \alpha} \right) \int \limits_{-\infty}^\infty \exp(-u^2) \mathrm{d} u = \\ & = \left(\cfrac{\pi}{\alpha}\right)^{3/2} \exp \left( -\cfrac{p^2}{4 \hbar^2 \alpha} \right) \end{split}$

что в итоге дает нам:

$\begin{split} & V(\mathbf{p}) = \\ & = -\cfrac{k}{\sqrt{8 \pi \hbar^3}} \int \limits_0^\infty \cfrac{\exp \left( -\cfrac{p^2}{4 \hbar^2 \alpha} \right)}{\alpha^2} \mathrm{d} \alpha = \\ & = \bigg \rvert_{\alpha = p^2/(4\hbar^2 \gamma)} \left( - \cfrac{k}{\sqrt{2 \hbar/\pi}} \right) \left( \cfrac{1}{p^2} \right) \int \limits_0^\infty \exp(-\gamma) \mathrm{d} \gamma = \\ & = \left( - \cfrac{k}{\sqrt{2 \hbar/\pi}} \right) \left( \cfrac{1}{p^2} \right) \end{split}$

Другими словами, результат Фурье-преобразования потенциальной энергии, обратно пропорциональной расстоянию, представляет собой функцию, обратно пропоциональную квадрату импульса. Фурье-преобразование произведения потенциальной энергии на исходную волновую функцию есть не что иное, как свертка Фурье-преобразований сомножителей, поэтому итоговое уравнение Шрёдингера в импульсном пространстве имеет вид:

$\left( \cfrac{p^2}{2m} - E \right) \psi(\mathbf{p}) - \left( \cfrac{k}{2 \pi^2 \hbar} \right) \int \limits_{R^3} \cfrac{\psi(\mathbf{p}')}{|\mathbf{p} - \mathbf{p}'|^2} \mathrm{d}^3 \mathbf{p}' = 0$

[Заметим, что из-за выбранной нами нормировки исходного преобразования Фурье нам пришлось ввести в свертку Фурье-преобразований потенциальной энергии и волновой функции дополнительный множитель $1/\sqrt{8 \pi^3 \hbar^3}$ . Различные нормировки приводят к разным промежуточным результатам, что однако же не влияет на вид окончательного уравнения.]

Выдающаяся догадка Фока заключалась в том, что это интегральное уравнение эквивалентно четырехмерному уравнению Лапласа, ограниченного поверхностью 3-сферы, отображенной с помощью стереографической проекции на трехмерное пространство импульсов!

Стереографическая проекция 3-сферы радиуса s описывается выражением:

$S_4 (x, y, z, w) = \cfrac{2s}{s - w} (x, y, z)$

Мы проецируем 3-сферу на гиперплоскость, которая касается ее в точке “южного полюса”, (0,0,0,–s). Обратите внимание, что s в этом случае отличается от радиуса, который имел место при проецировании на круг скоростей, так как сейчас мы имеем дело с пространством импульсов, содержащих дополнительный множитель m. Но пока что мы будем считать s неким свободным параметром.

Используя в качестве отправной точки интеграл по R³ в импульсной версии уравнения Шрёдингера, мы хотим перейти к координатам на 3-сфере. Эти координаты мы будем обозначать η, θ и φ, где:

$0 \leqslant \eta \leqslant \pi$
$0 \leqslant \theta \leqslant \pi$
$0 \leqslant \varphi \leqslant 2\pi$
Декартовы координаты имеют вид: $s (\sin \eta \sin \theta \cos \varphi, \sin \eta \sin \theta \sin \varphi, \sin \eta \cos \theta, \cos \eta)$
Элемент 3-объема $\mathrm{d}\Omega = s^3 \sin^2 \eta \sin \theta \mathrm{d}\eta \mathrm{d} \theta \mathrm{d} \varphi$
Полный объем 3-сферы = $2\pi^2 s^3$

Если мы рассмотрим проекцию произвольной точки $\mathbf{s} = s (\sin \eta \sin \theta \cos \varphi, \sin \eta \sin \theta \sin \varphi, \sin \eta \cos \theta, \cos \theta)$ , то окажется, что:

$S_4(\mathbf{s}) = \cfrac{2s \sin \eta}{1 - \cos \eta} (\cos \varphi \sin \theta, \sin \varphi \sin \theta, \cos \theta)$

Две угловых сферических координаты в R³, θ и φ, в точности совпадают с соответствующими координатами на 3-сфере, в то время как радиальная координата R³ (которую мы будем обозначать p, так как речь идет о пространстве импульсов) связана с угловой координатой η соотношением:

$p = \cfrac{2s \sin \eta}{1 - \cos \eta}$

Вскоре нам понадобится производная этого выражения, которая равна:

$\cfrac{\mathrm{d}p}{\mathrm{d}\eta} = -\cfrac{2s}{1 - \cos \eta}$

При переходе от p к η элемент 3-объема в импульсном пространстве принимает вид:

$\begin{split} & \mathrm{d}^3 \mathbf{p} = \\ & = p^2 \sin \theta \mathrm{d}p \mathrm{d} \theta \mathrm{d} \varphi = \\ & = \cfrac{4s^2 \sin^2 \eta}{(1 - \cos \eta)^2} \left| \cfrac{\mathrm{d}p}{\mathrm{d}\eta} \right| \sin \theta \mathrm{d} \eta \mathrm{d} \theta \mathrm{d} \varphi = \\ & = \cfrac{8s^3 \sin^2 \eta}{(1 - \cos \eta)^3} \sin \theta \mathrm{d} \eta \mathrm{d} \theta \mathrm{d} \varphi = \\ & = \cfrac{8}{(1 - \cos \eta)^3} \mathrm{d} \Omega \end{split}$

Мы можем переформулировать функцию η, заметив, что:

$\begin{split} & p^2 + 4s^2 = \\ & = 4s^2 \left( 1 + \cfrac{\sin^2 \eta}{(1 - \cos \eta)^2} \right) = \\ & = 4s^2 \left( \cfrac{1 - 2 \cos \eta + \cos^2 \eta + \sin^2 \eta}{(1 - \cos \eta)^2} \right) = \\ & = 8s^2 \left( \cfrac{1 - \cos \eta}{(1 - \cos \eta)^2} \right)= \\ & = \cfrac{8s^2}{1 - \cos \eta} \end{split}$

Следовательно:

$\mathrm{d}^3\mathbf{p} = \left( \cfrac{p^2}{4s^2} + 1 \right)^3 \mathrm{d}\Omega$

Обратная проекция точки (X, Y, Z) трехмерной гиперплоскости в точку 3-сферы выражается формулой:

$R_4(X, Y, Z) = \cfrac{4s^2 X, 4s^2 Y, 4s^2 Z, s (X^2 + Y^2 + Z^2 - 4s^2)}{X^2 + Y^2 + Z^2 + 4s^2}$

Отсюда следует, что:

$\left| \mathbf{p} - \mathbf{p}' \right|^2 = \left( \cfrac{p^2}{4s^2} + 1 \right) \left( \cfrac{p'^2}{4s'^2} + 1 \right) \left| R_4(\mathbf{p}) - R_4(\mathbf{p'}) \right|^2$

Если мы обозначим s=R₄(p) и s‘=R₄(p‘), и введем функцию:

$\Psi(\mathbf{s}) = \left( \cfrac{p^2}{4s^2} + 1 \right)^2 \psi(\mathbf{p})$

то наш исходный интеграл по пространству R³ примет вид:

$\int \limits_{R^3} \cfrac{\psi(\mathbf{p}')}{|\mathbf{p} - \mathbf{p}'|^2} \mathrm{d}^3 \mathbf{p}' =\cfrac{1}{\cfrac{p^2}{4s^2} + 1} \int \limits_{sS^3} \left( \cfrac{\Psi(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \right) \mathrm{d}\Omega'$

Через sS³здесь обозначена поверхность шара радиуса s, где S³ – единичная 3-сфера в пространстве R⁴. Мы полагаем s равным $\sqrt{-Em/2}$ , что ровно в m раз больше значения, использовавшегося для пространства скоростей. Это означает, что:

$-E = \cfrac{2s^2}{m}$

$\cfrac{p^2}{2m} - E = \left( \cfrac{2s^2}{m} \right) \left( \cfrac{p^2}{4s^2} + 1 \right)$

В результате уравнение Шрёдингера в импульсном пространстве приводится к виду:

$\Psi(\mathbf{s}) - \left( \cfrac{m}{2s^2} \right) \left( \cfrac{k}{2\pi^2 \hbar} \right) \int \limits_{sS^3} \left( \cfrac{\Psi(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \right) \mathrm{d} \Omega' = 0$

Это уравнение инвариантно относительно любых четырехмерных поворотов: если Ψ(s) является его решением, а R – поворот в пространстве R⁴, то решением будет и Ψ_R(s)=Ψ(Rs). Для доказательства нам нужно просто сделать замену переменной интегрирования и перейти от s‘ к s”=R s‘, что не влияет ни на элемент объема, ни на область интегрирования, но при этом дает нам |s–s‘|=|R s–R s‘|=|R s–s”|.

Теперь рассмотрим функцию:

$P(\mathbf{r}, \mathbf{s}) = \cfrac{1}{|\mathbf{r} - \mathbf{s}|^2} = \cfrac{1}{(\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s})}$

где r и s – векторы в пространстве R⁴. Мы утверждаем, что P(r, s) удовлетворяет четырхмерному уравнению Лапласа, если считать s фиксированным и интерпретировать P(r, s) как функцию одного четырехмерного вектора r. Чтобы в этом убедиться, рассмотрим для начала производные по одной из координат – скажем, x, считая, что r=(x, y, z, w) и s=(s_x, s_y, s_z, s_w).

$\partial_x P(\mathbf{r}, \mathbf{s}) = -\cfrac{2(x - s_x)}{(\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s})}$

$\partial_{xx} P(\mathbf{r}, \mathbf{s}) = -\cfrac{2}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^2} + \cfrac{8(x - s_x)^2}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^3}$

Суммируя аналогичные слагаемые для всех четырех координат, имеем:

$\nabla^2 P(\mathbf{r}, \mathbf{s}) = -\cfrac{8}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^2} + \cfrac{8((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^3} = 0$

Вычисления проходят гладко, когда r ≠ s, но P(r, s), очевидно, имеет особенность при r = s. В общем случае ∇²P(r, s) не равно нулю, а имеет вид:

$\nabla^2 P(\mathbf{r}, \mathbf{s}) = -4\pi^2 \delta(\mathbf{r} - \mathbf{s})$ ,

где δ – дельта-функция Дирака, обобщенная функция, обладающая следующим свойством: интеграл от произведения любой “проверочной функции” f(r) на дельта-функцию Дирака δ(r – s) равен значению f при r=s. Мы не станем приводить строгое доказательство этого утверждения, но для придания ему большей правдоподобности заметим вначале, что градиент P(r, s) выражается формулой:

$\nabla P(\mathbf{r}, \mathbf{s}) = -\cfrac{2(\mathbf{r} - \mathbf{s})}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^2}$

Чтобы проинтегрировать лапласиан по единичному шару в R⁴ с центром в точке s (мы обозначим его s+B⁴, где B⁴ – единичный шар с центром в начале координат), вначале обратим внимание на то, что оператор Лапласа совпадает с дивергенцией градиента, а затем применим формулу Гаусса-Остроградского, чтобы представить результат в виде интеграла по трехмерной границе шара. Эта граница представляет собой единичную 3-сферу, s+S³, а единичная нормаль, направленная наружу шара, в любой точке границы r совпадает с r – s. Таким образом:

$\begin{split} & \int \limits_{\mathbf{s} + B^4} \nabla^2 P(\mathbf{r}, \mathbf{s}) \mathrm{d}^4 r = \\ & = \int \limits_{\mathbf{s} + B^4} \nabla \cdot \nabla P(\mathbf{r}, \mathbf{s}) \mathrm{d}^4 r = \\ & = \int \limits_{\mathbf{s} + S^3} (\mathbf{r} - \mathbf{s}) \cdot \nabla P(\mathbf{r}, \mathbf{s}) \mathrm{d} \Omega = \\ & = -2 \int \limits_{\mathbf{s} + S^3} \mathrm{d} \Omega = \\ & = -4 \pi^2 \end{split}$

Поскольку P(r, s) является решением уравнения Лапласа – как минимум при r ≠ s, а Ψ(s), входящая в наше уравнение на 3-сфере, представляет собой интеграл от P(s, s‘) по переменной s‘, кажется вполне разумным предположить, что уравнению Лапласа должна удовлетворять и сама функция Ψ(s). Чтобы сделать следующий шаг в поиске точного набора решений, мы подставим четырехмерную сферическую функцию:

$\Psi(\mathbf{s}) = Z_{\lambda, \sigma, \mu}(\mathbf{s})$

в наше преобразованное уравнение Шрёдингера на 3-сфере sS³. Для решения интеграла $\int \limits_{sS^3} \cfrac{Z_{\lambda, \sigma, \mu}(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \mathrm{d} \Omega'$ воспользуемся одним из вариантов второй формулы Грина, который является непосредственным следвием формулы Гаусса-Остроградского:

$\int \limits_V (f \nabla^2 g - g \nabla^2 f) \mathrm{d}^4 r = \int \limits_{\partial V} \mathbf{n} \cdot (f \nabla g - g \nabla f) \mathrm{d} \Omega$

Здесь n – единичная нормаль к четырехмерной области интегрирования V, направленная наружу поверхности. Чтобы воспользоваться этим тождеством, мы полагаем f = Z_{λ, σ, μ} и g=P(s‘, s)=1/|s–s‘|². Вместо интегрирования по всему четырехмерному шару sB⁴ мы исключим из него окрестность точки s с радиусом ε, а затем устремим ε к нулю. Другими словами, наша область интегрирования имеет вид:

$V = \{ \mathbf{s}' \in R^4 \rvert |\mathbf{s}'| \leqslant s, |\mathbf{s} - \mathbf{s}'| \geqslant \varepsilon \}$

Это дает нам преимущество, поскольку в пределах V обе функции f и g являются решениями уравнения Лапласа и, следовательно, левая часть формулы Грина, представляющая собой интеграл от содержащего лапласиан выражения по области V, обращается в нуль. В итоге мы получаем:

$\int \limits_{\partial V} Z_{\lambda, \sigma, \mu}(\mathbf{s}') (\mathbf{n} \cdot \nabla P(\mathbf{s}', \mathbf{s})) \mathrm{d} \Omega' = \int \limits_{\partial V} P(\mathbf{s}', \mathbf{s}) (\mathbf{n} \cdot \nabla Z_{\lambda, \sigma, \mu}(\mathbf{s}')) \mathrm{d} \Omega'$

Граница V состоит из двух частей. Одна из них – это 3-сфера sS³ за вычетом точек, удаленных от s на расстояние меньше ε. Вторую можно приближенно представить в виде 3-полусферы радиуса ε с центром в точке s.

На 3-сфере sS³ скалярное произведение наружной нормали n на градиент шаровой функции совпадает с производной шаровой функции по расстоянию от начала координат. С учетом однородности многочлена в результате получается исходная функция, домноженная на некоторую константу:

$\begin{split} & \mathbf{n} \cdot \nabla Z_{\lambda, \sigma, \mu}(\mathbf{s}') = \\ & = \partial_r Z_{\lambda, \sigma, \mu}\left( r \left( \cfrac{\mathbf{s}'}{s} \right) \right) \bigg \rvert_{r = s} = \\ & = \partial_r \left( r^\lambda Y_{\lambda, \sigma, \mu}\left( \cfrac{\mathbf{s}'}{s} \right) \right) \bigg \rvert_{r = s} = \\ & = \lambda r^{\lambda - 1} Y_{\lambda, \sigma, \mu}\left( \cfrac{\mathbf{s}'}{s} \right) \bigg \rvert_{r = s} = \\ & = \cfrac{\lambda}{s} Z_{\lambda, \sigma, \mu}(\mathbf{s}') \end{split}$

Аналогичный результат имеет место и в случае функции P(s‘, s), если мы опять-таки вычислим скалярное произведение наружной нормали n и ее градиента на 3-сфере s S³:

$\nabla P(\mathbf{r}, \mathbf{s}) = -\cfrac{2(\mathbf{r} - \mathbf{s})}{((\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s}))^2}$

$\cfrac{\mathbf{r}}{r} \nabla P(\mathbf{r}, \mathbf{s}) \bigg \rvert_{r=s} = -\cfrac{2}{s} \cfrac{s - \mathbf{r} \cdot \mathbf{s}}{(2s - 2 \mathbf{r} \cdot \mathbf{s})^2} = -\cfrac{1}{2s(s - \mathbf{r} \cdot \mathbf{s})}$

$P(\mathbf{r}, \mathbf{s}) \bigg \rvert_{r=s} = \cfrac{1}{(\mathbf{r} - \mathbf{s}) \cdot (\mathbf{r} - \mathbf{s})} \bigg \rvert_{r=s} = \cfrac{1}{2(s - \mathbf{r} \cdot \mathbf{s})}$

Подставляя r=s‘, имеем на 3-сфере sS³:

$\mathbf{n} \cdot \nabla P(\mathbf{s}', \mathbf{s}) = -\cfrac{1}{s} P(\mathbf{s}', \mathbf{s})$

Вторую часть границы V можно (приближенно) представить в виде 3-полусферы с центром в точке s и радиусом ε. Интеграл от скалярного произведения наружной нормали на градиент ∇P(s‘, s) по любой полной 3-сфере с центром в s будет равен –4 π², как мы уже выяснили в ходе доказательства того, что лапласиан P пропорционален дельта-функции Дирака. Поскольку P(s‘, s) радиально симметрична относительно s, то по мере того, как ε стремится к нулю, один из интегралов по этой части границы V будет стремиться к:

$\int Z_{\lambda, \sigma, \mu}(\mathbf{s}') (\mathbf{n} \cdot \nabla P(\mathbf{s}', \mathbf{s})) \mathrm{d} \Omega' \rightarrow 2 \pi^2 Z_{\lambda, \sigma, \mu}(\mathbf{s})$ ,

где интегрирование ведется по 3-полусфере с центром в s.

В данном случае мы берем половину интеграла от нормального градиента P и меняем его знак, поскольку интегрирование ведется только по половине сферы, а наружная нормаль V антипараллельна наружной нормали 3-сферы с центром в s, которую мы исключаем из V. В пределе при ε, стремящемся к нулю, мы можем считать Z_{λ, σ, μ}(s‘) постоянной во всей области интегрирования, заменяя ее конкретным значением Z_{λ, σ, μ}(s).

Второй интеграл, требующий рассмотрения, имеет вид:

$\int P(\mathbf{s}', \mathbf{s}) (\mathbf{n} \cdot \nabla Z_{\lambda, \sigma, \mu}(\mathbf{s'})) \mathrm{d} \Omega' \rightarrow \cfrac{\pi^ \varepsilon^3}{\varepsilon^2} (\mathbf{n} \cdot \nabla Z_{\lambda, \sigma, \mu}(\mathbf{s'})) \bigg \rvert_{s' = s} \rightarrow 0$

где интегрирование опять-таки ведется по 3-полусфере с центром в s.

Так как объем 3-полусферы, представляющей собой область интегрирования, по мере уменьшения ε падает быстрее, чем растет P(s‘, s), интеграл стремится к нулю.

При ε, стремящемся к нулю, интегралы по 3-сфере sS³, исключающей некоторую малую окрестность точки s, будут стремиться к тем же самым интегралам, взятым по целой 3-сфере. Сводя все результаты вместе, получаем:

$2\pi^2 Z_{\lambda, \sigma, \mu}(\mathbf{s}) - \cfrac{1}{s} \int \limits_{sS^3} \left( \cfrac{Z_{\lambda, \sigma, \mu}(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \right) \mathrm{d} \Omega' = \cfrac{\lambda}{s} \int \limits_{sS^3} \left( \cfrac{Z_{\lambda, \sigma, \mu}(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \right) \mathrm{d} \Omega'$

$Z_{\lambda, \sigma, \mu}(\mathbf{s}) - \cfrac{\lambda + 1}{2 \pi^2 s} \int \limits_{sS^3} \left( \cfrac{Z_{\lambda, \sigma, \mu}(\mathbf{s}')}{|\mathbf{s} - \mathbf{s}'|^2} \right) \mathrm{d} \Omega' = 0$

Чтобы это равенство совпало с уравнением, которое мы хотим решить, должно выполняться условие:

$\left( \cfrac{m}{2s^2} \right) \left( \cfrac{k}{2\pi^2 \hbar} \right) = \cfrac{\lambda + 1}{2 \pi^2 s}$

$s = \cfrac{mk}{2\hbar (\lambda + 1)}$

Поскольку E = –2 s² / m, отсюда следует, что квантовая система имеет энергетические уровни:

$E = -\cfrac{mk^2}{2\hbar^2 (\lambda + 1)^2}$ ,

где λ+1 – положительное число. Как мы и надеялись, этот результат в точности совпадает с формулой, полученной путем обычного решения уравнения Шрёдингера. Когда речь идет об описании энергетических уровней водородного атома, квантовое число, которое мы обозначили как λ+1, обычно записывают буквой n.

В рамках метода Фока степень “вырожденности” энергетического уровня – количество независимых собственных функций, соответствующих конкретному значению n – совпадает с размерностью пространства однородных многочленов степени λ, зависящих от четырех переменных и удовлетворяющих уравнению Лапласа. Ранее мы показали, что эта величина равна (λ+1)² = n², что совпадает со степенью вырожденности, найденной обычными методами.

Обычный способ классификации отдельных состояний, составляющих каждый энергетический уровень, основан на использовании квантового числа l, такого, что ℏ² l(l+1) является собственным значением L², и квантового числа m (которое не следует путать с массой частицы), такого, что mℏ является собственным значением L_z. Исходя из наших знаний об алгебре трехмерных поворотов, m может принимать целочисленные значения в интервале от –l до l, что дает в общей сложности 2l+1 состояний. Изучив механизм сложения двух независимых спинов, можно показать, что в силу соотношения L = A + B квантовое число l может принимать значения в диапазоне от |λ_A – λ_B| до λ_A + λ_B. Но поскольку λ_A=λ_B=½λ, допустимые значения l составляют интервал от 0 до λ. Таким образом, общее количество состояний равно:

$1 + 3 + 5 + \dots + (2\lambda + 1) = (\lambda + 1)^2 = n^2$ ,

что совпадает с ранее полученным результатом.

Заметим, что функции Z_{λ, σ, μ} являются собственными функциями операторов A² = B²:

$A^2 Z_{\lambda, \sigma, \mu}(\mathbf{r}) = B^2 Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \hbar^2 \left( \cfrac{\lambda}{2} \right) \left( \cfrac{\lambda}{2} + 1 \right) Z_{\lambda, \sigma, \mu}(\mathbf{r})$

а также операторов A_z и B_z, и, как следствие, L_z = A_z + B_z:

$A_z Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \sigma \hbar Z_{\lambda, \sigma, \mu}(\mathbf{r})$

$B_z Z_{\lambda, \sigma, \mu}(\mathbf{r}) = \mu \hbar Z_{\lambda, \sigma, \mu}(\mathbf{r})$

$L_z Z_{\lambda, \sigma, \mu}(\mathbf{r}) = (\sigma + \mu) \hbar Z_{\lambda, \sigma, \mu}(\mathbf{r})$ ,

но при этом не являются собственными функциями L². Поэтому, несмотря на то, что мы можем соотнести λ+1 со стандартным квантовым числом n, а σ + μ – со стандартным квантовым числом m, функциям Z_{λ, σ, μ}, вообще говоря, не соответствуют какие-либо конкретные значения стандартного квантового числа l. Чтобы получить функции, которые характеризуются определенными значениями чисел m и l, нам пришлось бы рассмотреть соответствующие линейные комбинации всех Z_{λ, σ, μ}, удовлетворяющих условию σ + μ = m.

Литература

[1] W. Pauli. Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. Zeitschrift für Physik 36: 336–363 (1926).

[2] Leonard I. Schiff. Quantum Mechanics. – McGraw-Hill, 1968 (параграф 30).

[3] V. Fock, Zur Theorie des Wasserstoffatoms. Zeitschrift für Physik 98: 145–154 (1935).

[4] Jonas Karlsson. The SO(4) symmetry of the hydrogen atom, University of Minnesota, 14 December 2010. Доступно в сети по адресу: в формате PDF.

[5] Radosław Szmytkowski. Solution of the momentum-space Schrödinger equation for bound states of the N-dimensional Coulomb problem (revisited). Доступно в сети в виде препринта arXiv.

[6] M. Bander, C. Itzykson. Group theory and the hydrogen atom (I). Rev. Mod. Phys. 38: 330–345 (1966).

Рубрика: Грег Иган. Статьи

Эллипсы и атомы