Стрелы времени. Приложение 3. Мягкий перехват

Оригинал:
http://www.gregegan.net/ORTHOGONAL/E3/SoftInterception.html

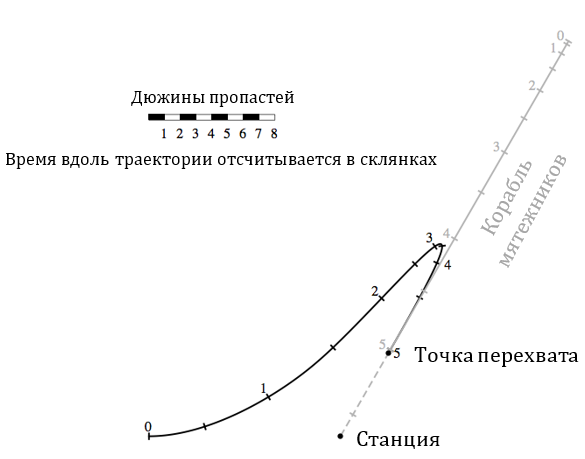
В третьей главе перед Рамиро и Тарквинией встает необходимость перехватить неподконтрольный им космический корабль, который движется с ускорением вдоль фиксированной траектории. Их цель – попасть на борт судна, поэтому просто оказаться у него на пути недостаточно – нужно еще и сравняться с ним в скорости. Это и есть мягкий перехват.

По какой траектории должны двигаться герои, чтобы как можно быстрее осуществить перехват корабля мятежников, учитывая, что их собственные двигатели могут сколь угодно долго поддерживать режим максимальной тяги? Поскольку скорости, о которых идет речь, не настолько велики, чтобы вызвать какие-либо релятивистские эффекты, альтернативная физика Ортогональной Вселенной в данном случае себя никак не проявляет (не считая того, что именно благодаря ей работают двигатели этих кораблей, которые создают кинетическую энергию за счет излучения света и не нуждаются ни в топливе, ни в рабочем теле). Это означает, что мы можем воспользоваться теми же самыми законами Ньютона, которые действуют в нашей Вселенной при малых скоростях.

Подобная задача – определение математической функции, при которой заданная величина достигает минимума или максимума – решается с помощью вариационного исчисления. В данном случае интересующая нас функция будет описывать траекторию в пространстве как функцию времени, а величина, значение которой мы хотим минимизировать, представляет собой время, необходимое, чтобы добраться по этой траектории от начального местоположения москита-преследователя до некоторой точки, лежащей на траектории мятежного корабля.

Предположим, что в момент начала погони положение москита Рамиро и Тарквинии характеризуется вектором p₀, его скорость – вектором v₀, а максимальное ускорение, которое могут выдать их двигатели равно A. Корабль мятежников движется по прямой с постоянным ускорением; если мы обозначим соответствующий вектор ускорения через a, то траектория корабля как функция времени описывается уравнением:

$\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{w}_0 t + \cfrac{\mathbf{a} t^2}{2}$

Мы будем вести отсчет времени с момента начала погони, поэтому при t=0 преследующий москит характеризуется радиус-вектором p₀ и скоростью v₀, в то время как корабль мятежников имеет радиус-вектор r₀ и движется со скоростью w₀.

К каждой из возможных траекторий преследующего москита, p(t) мы предъявляем следующие требования:

p(0) = p₀ – чтобы траектория начиналась в нужном нам месте.
p‘(0) = v₀ – чтобы в начале траектории москит двигался с нужной нам скоростью.
p(T) = r(T) в некоторый момент времени T, чтобы преследователь догнал корабль мятежников.
p‘(T) = r’(T) при том же самом T, чтобы в этот момент оба москита двигались с одной и той же скоростью.
|p’’(T)| ⩽ A при всех 0 ⩽ t ⩽ T, чтобы преследующему москиту не пришлось ускоряться сверх своих возможностей.

Наша цель – найти такую траекторию p(t), при которой время T, необходимое на перехват, достигает минимального значения с учетом приведенных выше ограничений.

Мы слегка упростим наш анализ, предположив без доказательства, что преследующий москит должен поддерживать максимальную тягу своих двигателей в течение всего пути, меняя лишь направление своего выхлопа. Интуиция подсказывает, что движение с максимально возможным ускорением непременно принесет какую-то выгоду (более обстоятельный анализ это подтверждает). Благодаря этому допущению, неравенство в последнем условии можно заменить равенством:

|p’’(T)| = A при всех 0 ⩽ t ⩽ T – иначе говоря, преследующий москит на всем протяжении пути движется с максимальным ускорением – не больше и не меньше.

Это условие также можно представить в виде:

$\mathbf{p}''(t) \cdot \mathbf{p}''(t) - A^2 = 0$

Так вот, если бы речь шла о задаче из области обыкновенного математического анализа, то для поиска минимума функции F(x, y, z) с учетом некоторого ограничения, представленного, к примеру, в виду G(x, y, z)=0, мы бы воспользовались следующим приемом, известным как метод множителей Лагранжа. Предположим, что нам удалось решить уравнение G(x, y, z)=0 относительно одной из переменных – скажем, z. Тогда мы могли бы написать:

$f(x, y) = F(x, y, z(x, y))$

и стали бы искать минимум f(x, y), приравняв к нулю ее частные производные по x и y:

$\partial_x f(x, y) = \partial_x F + \partial_z F \partial_x z = 0$
$\partial_y f(x, y) = \partial_y F + \partial_z F \partial_y z = 0$

Кроме того, мы можем взять производные G(x, y, z(x, y)) по x и y, которые, разумеется, должны быть равны нулю, поскольку z=z(x, y) является решением уравнения G(x, y, z)=0.

$\partial_x G + \partial_z G \partial_x z = 0$
$\partial_y G + \partial_z G \partial_y z = 0$

В общей сложности это дает нам четыре уравнения. Выразив из последних двух равенств ∂_xz и ∂_yz и подставив результат в первую пару уравнений, имеем:

$\partial_x F - \cfrac{\partial_z F}{\partial_z G} \partial_x G = 0$
$\partial_y F - \cfrac{\partial_z F}{\partial_z G} \partial_y G = 0$

Однако тот же самый результат можно было бы получить из трех уравнений:

$\partial_x F + \lambda \partial_x G = 0$
$\partial_y F + \lambda \partial_y G = 0$
$\partial_z F + \lambda \partial_z G = 0$

решив последнее относительно λ, что в результате дало бы нам:

$\lambda = - \cfrac{\partial_z F}{\partial_z G}$

Таким образом, наша первоначальная задача эквивалентная нахождению точек, в которых производные функции

$S(x, y, z, \lambda) = F(x, y, z) + \lambda G(x, y, z)$

по x, y, z и λ одновременно обращаются в нуль, причем в случае производной по λ мы просто получаем наше исходное ограничение G(x, y, z)=0. Дополнительная переменная λ называется множителем Лагранжа.

Для более полного понимания данную ситуацию можно описать в геометрических терминах. Градиент функции F имеет вид ∇F=(∂_xF, ∂_yF, ∂_zF) и представляет собой вектор, перпендикулярный «изоповерхностям» или «множествам уровня» функции F – то есть множествам точек пространства (x, y, z), в которых функция F принимает одно и то же значение. Градиент функции G аналогичным образом имеет вид ∇G=(∂_xG, ∂_yG, ∂_zG) и направлен под прямым углом к множествам, в пределах которых G остается постоянной – включая, разумеется, и множество точек, удовлетворяющих уравнению G(x, y, z)=0. Приведенную выше тройку уравнений, связывающих между собой частные производные функций F и G, можно представить в виде единого соотношения, выраженного через соответствующие градиенты:

$\nabla F = -\lambda \nabla G$

Если некоторый путь начинается в точке множества, которое удовлетворяет ограничивающему уравнению, и не выходит за пределы этого множества, то касательные к нему будут перпендикулярны ∇G. Но если ∇F отличается от ∇G лишь множителем, тот же самый касательный вектор будет перпендикулярен и ∇F, а значит, при движении вдоль этого пути F будет сохранять постоянное значение. Следовательно, выполнение ограничения в такой точке гарантирует обращение в нуль производной F, как и должно быть в окрестности локального максимума или минимума.

Сказанное легко обобщается на любое количество ограничивающих функций G₁, G₂, G₃, …, которые должны одновременно обращаться в нуль в некотором пространстве с любым числом переменных. Двигаясь вдоль пути, который начинается в точке, удовлетворяющей всем этим ограничениям, и одновременно перпендикулярен к ∇G₁, ∇G₂, ∇G₃ … мы гарантируем выполнение всех ограничений и в остальных точках пути. Предположим теперь, что в некоторой точке множества, заданного набором ограничений, имеет место равенство:

$\nabla F = -\lambda_1 \nabla G_1 - \lambda_2 \nabla G_2 -\lambda_3 \nabla G_3 - \dots$

Поскольку касательная к любому пути, который проходит через такую точку и находится в множестве, удовлетворяющем данным ограничениям, будет перпендикулярна каждому из векторов ∇G_i, то та же самая касательная будет перпендикулярна и вектору ∇F. Отсюда следует, что производная F вдоль любого такого пути будет равна нулю, что делает соответствующую точку кандидатом на роль локального максимума или минимума F с учетом ограничений G₁ = G₂ = G₃ … = 0.

Вернемся к исходной задаче. Наша цель – наложить ограничение:

$\mathbf{p}''(t) \cdot \mathbf{p}''(t) - A^2 = 0$

на всю траекторию преследующего москита. Если мы будем считать, что каждое значение t требует отдельного ограничения, то нам нужно «просуммировать» произведения индивидуальных множителей Лагранжа и соответствующего ограничения для всех моментов времени. Но в случае непрерывных значений такого рода сумма заменяется интегралом. Иными словами, мы записываем интеграл, который включает в себя как промежуток времени, затраченного на движение вдоль траектории (именно эту функцию мы хотим свести к минимуму), так и произведение множителя Лагранжа на нашу ограничивающую функцию с учетом того, что множитель Лагранжа теперь является функцией времени:

$\displaystyle I(\mathbf{p}, \lambda) = \int \limits_0^{T(\mathbf{p})} (1 + \lambda(t)(\mathbf{p}''(t) \cdot \mathbf{p}''(t) - A^2)) dt$

В данном случае интеграл от 1, взятый вдоль конкретной траектории, характеризует суммарные затраты времени. Верхний предел этого интеграла мы представили в виде T(p), чтобы подчеркнуть тот факт, что момент перехвата будет зависеть от выбора траектории. Фактическое значение T(p) совпадает с первым положительным решением уравнения:

$\mathbf{p}(T) = \mathbf{r}(T)$

Наша цель – определить траекторию p_M(t), которая минимизирует время перехвата с учетом всех введенных нами ограничений, и для ее достижения мы найдем p_M(t) вместе с соответствующим множителем Лагранжа λ_M(t), таким, что производная интеграла I(p, λ) относительно любой допустимой вариации в любой из функций равна нулю. Вариация считается допустимой, если она не нарушает соответствие траектории необходимым граничным условиям: новая траектория, во-первых, должна иметь те же самые начальные координаты и скорость, а во-вторых, должна пересечь траекторию корабля мятежников так, чтобы корабль героев оказался в той же точке и двигался с той же скоростью, что и преследуемый москит. Мы будем рассматривать траектории вида:

$\mathbf{p}(t) = \mathbf{p}_M(t) + \varepsilon \mathbf{q}(t)$

где для удовлетворения граничных условий при t=0 мы введем ограничения:

$\mathbf{q}(0) = 0$
$\mathbf{q}'(0) = 0$

Так как p_M (по определению) характеризуется корректными координатами и скоростью, данные ограничения гарантируют, что то же самое верно и для p_M + ε q. Мы требуем, чтобы в момент t=T:

$\mathbf{p}_M(t) + \varepsilon \mathbf{q}(t) = \mathbf{r}(t)$
$\mathbf{p}'_M(t) + \varepsilon \mathbf{q}'(t) = \mathbf{r}'(t)$

Имейте в виду, что T зависит от варьируемой траектории, поэтому первое уравнение не является ограничением q, а скорее, позволяет определить значение T, которое просто совпадает с его первым положительным решением.

Если мы продифференцируем эту пару уравнений по ε, а затем положим ε равным 0, то получим следующее соотношение (где T_M – это сокращенное обозначение T(p_M)):

$\mathbf{q}'(T_M) = (\mathbf{r}'(T_M) - \mathbf{p}'_M(T_M)) \cfrac{dT}{d\varepsilon} \mid_{\varepsilon = 0} = 0$

$\mathbf{q}''(T_M) = (\mathbf{r}''(T_M) - \mathbf{p}''_M(T_M)) \cfrac{dT}{d\varepsilon} \mid_{\varepsilon = 0} = (\mathbf{a} - \mathbf{p}''_M(T_M)) \cfrac{dT}{d\varepsilon} \mid_{\varepsilon = 0}$

Кроме того, мы будем варьировать и сам множитель Лагранжа, полагая:

$\lambda(t) = \lambda_M(t) + \varepsilon \mu(t)$

Теперь мы применим ограничение, в соответствии с которым производная нашего интеграла по ε равна нулю:

$\cfrac{d}{d\varepsilon}I(\mathbf{p}_M + \varepsilon \mathbf{q}, \lambda_M + \varepsilon \mu) \mid_{\varepsilon = 0} = 0$

Rendered by QuickLaTeX.com

Так как p_M по определению должно удовлетворять ограничению, требующему, чтобы модуль ускорения был всюду равен A, последнее равенство принимает вид:

$\displaystyle \cfrac{dT}{d \varepsilon} \mid_{\varepsilon = 0} + 2 \int \limits_0^{T_M} \lambda_M(t) \mathbf{p}''_M(t) \cdot \mathbf{q}''(t) dt = 0$

Данный интеграл можно преобразовать, используя правило интегрирования по частям, которое в общем случае имеет вид:

$\displaystyle \int \limits_a^b u(t) v'(t) dt = u(t) v(t) \mid_a^b - \int \limits_a^b u'(t) v(t) dt$

Дважды применяя это правило, чтобы перенести производные по t с q’’(t) на λ_M(t) p_M’’(t), имеем:

Rendered by QuickLaTeX.com

Граничные условия для q требуют, чтобы q(0) = 0, q‘(0) = 0 и, кроме того, q(T_M) = 0. Подставляя единственное отличное от нуля граничное условие q‘(T_M) = [a – p_M’’(T_M)] (dT/dε)|_ε=0, имеем:

Rendered by QuickLaTeX.com

Это уравнение должно выполняться для любой вариации q. Как нетрудно заметить, данный интеграл можно обратить в нуль для любого q, если произведение ускорения соответствующей траектории на множитель Лагранжа удовлетворяет дифференциальному уравнению:

$\cfrac{d^2}{dt^2}(\lambda_M(t) \mathbf{p}''_M(t)) = 0$

Если это уравнение обратится в тождество, нам также потребуется проследить за тем, чтобы граничный член был равен нулю сам по себе. Самый простой способ убедиться в том, что это возможно – просто решить уравнение, получив в результате:

$\lambda_M(t) \mathbf{p}''_M (t) = \mathbf{C} t + \mathbf{D}$

где C и D – некоторые векторы. Поскольку модуль ускорения вдоль траектории p_M равен постоянной величине A, то:

$|\lambda_M(t)| |\mathbf{p}''_M(t)| = |\mathbf{C} t + \mathbf{D}|$
$|\lambda_M(t)| A = |\mathbf{C} t + \mathbf{D}|$
$|\lambda_M(t)| = \pm \cfrac{|\mathbf{C} t + \mathbf{D}|}{A}$
$\mathbf{p}''_M(t) = \pm \cfrac{A(\mathbf{C} t + \mathbf{D})}{|\mathbf{C} t + \mathbf{D}|}$

Если для начала мы выберем конкретную пару векторов C и D, а затем умножим оба вектора на некоторую константу, то она сократится в выражении для p_M’’(t) и, следовательно, никак не повлияет на возможность выбора траектории, удовлетворяющей конкретным требованиям задачи: совпадения положения и скорости преследующего москита с положением и скоростью корабля мятежников в точке перехвата. Если мы теперь подставим наше решение в выражение для граничного члена, опустив общий множитель (dT/dε)|_ε=0, то:

Rendered by QuickLaTeX.com

Если мы введем обозначение:

$\mathbf{c} = \mathbf{C}T_M + \mathbf{D}$

а затем сделаем подстановку c → α c, то граничный член примет вид:

$1 + 2(\alpha \mathbf{c} \cdot \mathbf{a} - \pm A |\alpha||\mathbf{c}|)$

Если мы предположим, что α больше нуля, то граничный член можно обратить в нуль, положив:

$\alpha = \cfrac{1}{2(\pm A |\mathbf{c}| - \mathbf{c} \cdot \mathbf{a})}$

и выбрав подходящий знак (напомним, что от выбора знака зависит общее соотношение между ускорением траектории и направлением C t + D). Мы ожидаем, что в момент перехвата преследующий москит будет ускоряться примерно в том же самом направлении, что и корабль мятежников, поэтому знак «+» будет подходить в том случае, когда c · a положительно. Так как преследующий москит сможет догнать корабль мятежников только при условии A > |a|, знаменатель правой части должен быть больше нуля, откуда следует, что α, как и предполагалось, будет положительным. Если бы c · a было отрицательным, мы могли бы просто изменить направление изначально выбранных векторов C и D на противоположное.

Таким образом, мы можем обратить в нуль как граничный член, так и интеграл, при условии, что ускорение вдоль траектории имеет вид:

$\mathbf{p}''_M(t) = \cfrac{A(\mathbf{C} t + \mathbf{D})}{|\mathbf{C} t + \mathbf{D}|}$

Чтобы получить общее решение, мы вначале рассмотрим одно частное. (Следующие выкладки частично основаны на статье [2], посвященной задаче поиска пути, по которому должен двигаться раннер, обегающий базы во время бейсбольного матча, чтобы затратить на свой путь минимальное время.)

Функция гиперболического синуса, sh x, определяется следующим образом:

$\mathrm{sh} x = \cfrac{e^x - e^{-x}}{2}$

Обратную функцию, называемую ареасинусом, можно получить, решив квадратное уравнение относительно e^x и прологарифмировав результат:

$y = \mathrm{sh} x$
$2y = e^x - e^{-x}$
$(e^x)^2 - 2ye^x - 1 = 0$
$\mathrm{arsh} y = x = \ln(y + \sqrt{1 + y^2})$

Поскольку производная натурального логарифма – это функция, обращающая значение своего аргумента, то производная ареасинуса равна:

$(\mathrm{arsh} y)' = \cfrac{1 + \cfrac{y}{\sqrt{1 + y^2}}}{y + \sqrt{1 + y^2}} = \cfrac{1}{\sqrt{1 + y^2}}$

Благодаря этому, мы можем найти простую векторную функцию, первая производная которой имеет постоянный модуль A:

$\mathbf{V}(t) = \mathbf{V}_0 + A \left( \mathrm{arsh} t, \sqrt{1 + t^2} \right)$
$\mathbf{V}'(t) = A \left( \cfrac{1}{\sqrt{1 + t^2}}, \cfrac{t}{\sqrt{1 + t^2}} \right) = \cfrac{A(1, t)}{|(1, t)|}$
$|\mathbf{V}'(t)| = A$

Приложив еще немного усилий, можно взять интеграл от этой скорости:

$\mathbf{X}(t) = \mathbf{X}_0 + \mathbf{V}_0 t + A \left(t \mathrm{arsh} t - \sqrt{1 + t^2}, \cfrac{1}{2}\left(\mathrm{arsh} t + t \sqrt{1 + t^2} \right) \right)$

Чтобы обобщить этот результат, мы можем сделать подстановку t → β t + γ, одновременно заменив A на A/β², чтобы сохранить неизменным модуль ускорения. Кроме того, мы можем повернуть нашу систему координат на произвольный угол θ. В итоге у нас остается восемь параметров, значения которых можно варьировать: по два компонента векторов X₀ и V₀, а также величины β, γ, θ и время перехвата T. При этом должны удовлетворяться четыре уравнения в момент t=0 – чтобы положение и скорость преследующего москита в начальный момент соответствовали исходным данным, – и еще четыре в момент t=T – чтобы положение и скорость преследователей совпали с положением и скоростью корабля мятежников.

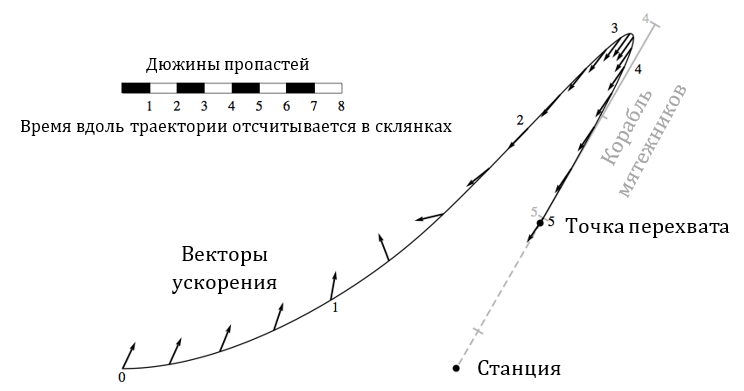
Решение этой системы уравнений можно найти численными методами. В результате получится кривая, которая и была приведена в романе – вдоль нее вектор ускорения сохраняет постоянный модуль, в то время как его направление меняется во времени.

Литература

Bendersky. The Calculus of Variations. Lecture Notes, City University of New York
http://math.hunter.cuny.edu/mbenders/cofv.pdf¹
Davide Carozza, Stewart Johnson and Frank Morgan. Baserunner’s Optimal Path. The Mathematical Intelligencer, October 2009
http://web.williams.edu/Mathematics/fmorgan/Baserunner.pdf²

М. Бендерски. Вариационное исчисление. Материалы лекций, Нью-Йоркский университет – прим. пер.
Дэвид Кароцца, Стюарт Джонсон, Фрэнк Морган. Оптимальный путь раннера, обегающего базы. Журнал «The Mathematical Intelligencer», октябрь 2009 г. – прим. пер.