Дважды плюс, дважды минус. Знакомство с физикой “Дихронавтов”

Оригинал статьи:
http://gregegan.net/DICHRONAUTS/00/DPDM.html

Окружающая нас четырехмерная Вселенная содержит три измерения пространства и одно измерение времени. Но каково было бы жить в мире, где эти роли распределены поровну – так что и пространство, и время содержат ровно по две размерности?

Может показаться, что при наличии двух размерностей времени история любых частиц и существ перестанет быть линейной и приобретет некий плоскостный аспект. В действительности же нет никаких причин, которые бы мешали телам двигаться по одномерным мировым линиям, подобно тому, как это имеет место в нашей Вселенной. Разница, проистекающая из двумерного характера времени, состоит в том, что теперь через заданную точку пространства могут проходить новые, запрещенные в нашей Вселенной, мировые линии.

Стоит нам выбрать конкретную мировую линию в качестве нашей индивидуальной линии времени, как оказывается, что перпендикулярное ей трехмерное пространство подчиняется довольно своеобразной геометрии, где роль, отведенную в нашей Вселенной окружностям и сферам, играют гиперболы и гиперболоиды, свет может двигаться лишь в строго определенных направлениях, а некоторые реки текут вверх. И это лишь некоторые из странных явлений, которые можно обнаружить в мире «Дихронавтов».

Мировые линии в пространстве “Дихронавтов”

Мировая линия – это кривая, которую с течением времени образуют координаты тела, принимаемого за идеализированную материальную точку. Точки самой мировой линии, однако же, отражают не только положение тела в пространстве, а описываются четырьмя координатами – включая момент времени, к которому тело достигает местоположения, заданного остальными тремя числами. Представить нечто подобное в четырех измерениях непросто, но если мы уберем одно из пространственных измерений, то сможем без труда изобразить мировые линии в получившемся трехмерном пространстве, как показано на следующем рисунке.

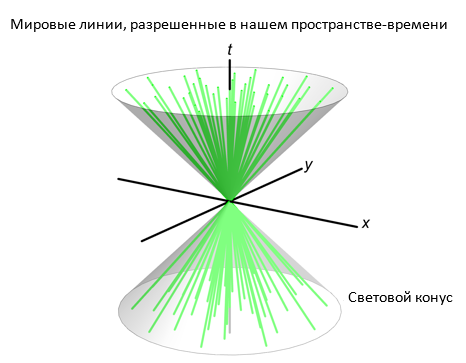
Время на таких пространственно-временных диаграммах обычно изображается в виде вертикальной оси. Таким образом, мировая линия неподвижного объекта будет иметь вид вертикальной прямой, в то время как для объекта, находящегося в состоянии равномерного и прямолинейного движения эта прямая будет отклоняться от вертикали под некоторым углом, а положение объекта при перемещении вверх по мировой линии – т. е. вперед во времени – будет меняться с постоянной скоростью.

Ведя речь о геометрии пространства-времени, единицы измерения зачастую выбирают так, чтобы скорость света в точности равнялась 1; к примеру, мы могли бы измерять время в годах, в расстояние – в световых годах. Если изобразить пространственно-временную диаграмму с учетом такой системы единиц, то окажется, что мировая линия тела, движущегося со скоростью света, будет всегда располагаться под углом 45⁰ к вертикали. На рисунке выше этот предел отмечен световым конусом. А поскольку обычные тела всегда движутся с досветовой скоростью, именно внутри светового конуса и должны находиться разрешенные мировые линии.

Условие нахождения внутри светового конуса можно выразить через четверку координат (x, y, z, t), характеризующих произвольную точку мировой линии. Поскольку x² + y² + z² есть не что иное, как квадрат полного пространственного расстояния от начала координат (в силу трехмерного аналога теоремы Пифагора), то в случае тела, движущегося с досветовой скоростью (которая при нашем выборе единиц равна 1), величина x² + y² + z² должна быть меньше квадрата прошедшего времени, t². В математической записи:

Слегка переставив слагаемые, мы можем привести это неравенство к виду:

Каждая из пространственных координат x, y, z входит в это неравенство со знаком плюс, в то время как перед единственной координатой времени t стоит знак минус. Таким образом, при переходе во вселенную с двумя измерениями пространства x, y и двумя измерениями времени t, u следует ожидать, что в аналогичном выражении будет два знака плюс и два знака минус:

Опустив одну из пространственных координат, y, допустимые мировые линии во вселенной «Дихронавтов» можно изобразить на трехмерном рисунке (см. ниже). В данном случае мировые линии не заключены внутри конуса с осью t, а находятся вне конуса с осью x. (Эта картина была бы полной, если бы речь шла о вселенной с единственной размерностью пространства, однако нам следует помнить о том, что в действительности у пространства есть и второе, не показанное на рисунке, измерение y. В четырех измерениях между разрешенными и запрещенными областями мировых линий имеет место идеальная симметрия.)

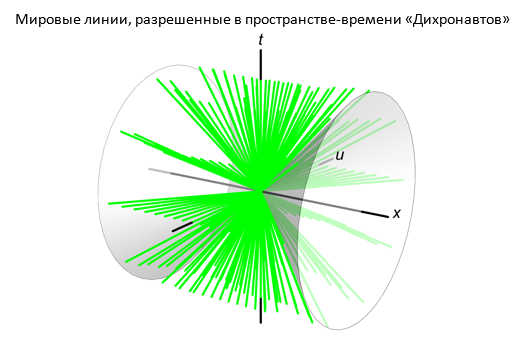
Так или иначе, приведенная выше диаграмма ясно показывает нам, что если мировые линии тел, движущихся вдоль оси x, по-прежнему не могут быть наклонены к оси t под углом больше 45⁰, то в случае тел, движущихся вдоль оси u, этот угол ничем не ограничен. Другими словами, в направлении оси u предела скоростей не существует! То же самое будет верно и для любого другого направления, расположенного ближе к u, чем к x.

Таким образом, понятие истории объекта как линейной последовательности событий – иначе говоря, его мировой линии – имеет смысл и во вселенной с двумя измерениями времени. Главное отличие касается тел, движущихся с большими скоростями, – знакомый нам верхний предел скоростей теперь действует далеко не во всех направлениях, что, в свою очередь, расширяет множество разрешенных мировых линий.

Геометрия и повороты в пространстве “Дихронавтов”

Хотя разнообразие мировых линий играет важную роль для тел, движущихся со сверхвысокими скоростями, скорость большинства предметов, с которыми мы сталкиваемся в повседневной жизни, составляет лишь крошечную долю скорости света. По сути это означает, что все подобные объекты, как и мы сами, обладают практически параллельными мировыми линиями. Мы можем принять направление вдоль нашей собственной мировой линии за пространственно-временную ось времени, и другие люди – мировые линии которых почти параллельны нашей собственной – будут в общем и целом согласны с таким выбором.

После того, как одно из направлений выбрано в качестве оси времени, все перпендикулярные ему прямые будут восприниматься как направления в пространстве. В нашей Вселенной мы получаем три пространственных измерения с абсолютно одинаковым поведением – между x, y и z нет никаких фундаментальных отличий.

Если же мы зафиксируем переменную t в качестве оси времени во вселенной «Дихронавтов», то в итоге получим набор из трех «пространственных измерений» x, y, u, между которыми существует принципиальное разница, ведь u, в отличие от x и y, представляет собой направление, вдоль которого может двигаться потенциальная мировая линия. А значит, несмотря на то, что пространство «Дихронавтов» также включает в себя три измерения, ожидать, что его геометрия будет совпадать с привычной нам геометрией евклидова пространства, нельзя.

Правило, которому мы следовали выше, переходя от формулы, описывающей разрешенные мировые линии в нашей Вселенной, к аналогичной формуле для мира «Дихронавтов», заключалось в замене z² на ‑u². В евклидовом пространстве x² + y² + z² есть не что иное, как квадрат расстояния между началом координат и точкой (x, y, z). Это дает нам основание предположить, что в трехмерном пространстве с двумя «пространственноподобными» измерениями x, y и одним «времениподобным» измерением u величина x² + y² – u² будет каким-то образом описывать расстояние между началом координат и точкой (x, y, u).

Если величина x² + y² – u² положительна, мы можем трактовать ее как квадрат расстояния от начала координат. Но как быть, если она отрицательна? В этом случае нам придется использовать в качестве расстояния квадратный корень противоположной величины, u² – x² – y².

Это может показаться странным, но вывод, сделанный в предыдущем абзаце, по сути говорит нам о том, что в данной геометрии существует два принципиально разных вида «расстояний» – те, для которых x² + y² – u² положительно, и те, для которых эта величина отрицательна. Впрочем, особого сюрприза в этом нет, поскольку именно расстояния второго рода наблюдаются при движении вдоль потенциальной мировой линии. Хотя наш выбор координат закрепляет направление мировой линии за переменной t, а большая часть окружающих людей и предметов, согласно нашему допущению, характеризуются мировыми линиями, сориентированными примерно в одном и том же направлении, сам факт, что некоторые из «пространственных» направлений – перпендикулярных оси t – могут выступать в качестве направлений мировых линий, в то время как другие – нет, уже оказывается достаточным для того, чтобы свойства векторов, относящихся к этим двум видам, качественно отличались друг от друга.

Собственно говоря, есть и третий случай – направления, для которых x² + y² – u² в точности равно нулю. В евклидовом пространстве x² + y² + z² обращается в нуль только при условии, что нулю равны и x, и y, и z – то есть лишь в начале координат (0, 0, 0). Выражение x² + y² – u², с другой стороны, обращается в нуль на поверхности целого конуса.

На рисунке ниже изображены все три типа поверхностей, точки которых равноудалены от начала координат. Красная, похожая на песочные часы, поверхность, соответствует положительным значениям . Две зеленых, чашеобразных поверхности описывают случай x² + y² – u² < 0. А пара расположенных между ними синих конусов служат решением уравнения x² + y² – u² = 0. (Поскольку все три поверхности полупрозрачны, конусы выглядят синими только в тех местах, где на них не накладываются другие поверхности.)

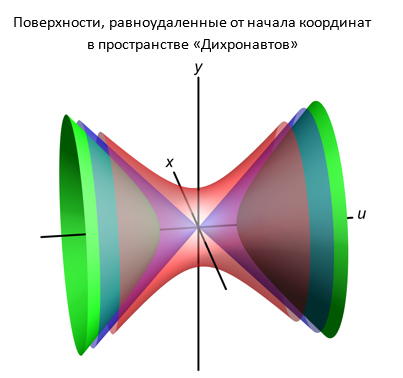
В математике красную поверхность принято называть однополостным гиперболоидом, а пару зеленых поверхностей – соответственно двуполостным гиперболоидом.

Описав новый способ измерения расстояний в нашей геометрии, можно задаться вопросом: что именно, с практической точки зрения, означает утверждение о равноудаленности точек каждой из этих поверхностей от начала координат. Говоря о вращении какого-либо предмета – раскручивании шара, взмахе палкой и вообще о повороте произвольного твердого тела – мы имеем в виду, что почти все точки затронутого предмета меняют свое положение, при том, что расстояния между этими точками остаются неизменными. Другими словами, объект при движении сохраняет жесткость – не сжимается и не растягивается.

Если мы взмахнем палкой, которая зафиксирована с одной стороны, то ее свободный конец всегда будет лежат на поверхности, равноудаленной от неподвижной точки – и в случае геометрии Евклида имеющей форму сферы. Таким образом, новые поверхности показывают нам, где мог бы оказаться свободный конец палки, если бы мы попытались проделать то же самое в геометрии «Дихронавтов».

Когда мы делаем взмах в пространстве «Дихронавтов», длина палки (по определению) остается постоянной, однако ее протяженность в конкретном направлении может расти без каких-либо ограничений! Например, если палка изначально имеет длину 5 и расположена вдоль оси u, мы можем повернуть ее так, чтобы свободный конец оказался в точке x=12, y=0, u=13, поскольку и в том, и в другом случае x² + y² – u² = -25. Если палка изначально имеет длину 5 и параллельна оси x, то мы аналогичным образом можем привести ее свободный конец в положение x=0, y=13, u=12, поскольку x² + y² – u² в обоих случаях равно 25. Но несмотря на то, что отдельные координаты могут принимать сколь угодно большие значения, связывающее их соотношение не позволяет повернуть первую палку так, чтобы ее положение совпало с одним из возможных положений второй, и наоборот.

При повороте тела в двух измерениях его поведение будет зависеть от того, являются ли оба измерения «пространственноподобными», как, например, x и y, или же парой «пространственноподобного» и «времениподобного» – как x и u. В первом случае результат будет выглядеть точно так же, как поворот в евклидовом прстранстве. Во втором – линии, равноудаленные от центра вращения будут иметь форму не окружностей, а гипербол, и протяженность тела вдоль одной из одной из осей может меняться в бесконечных пределах.

На следующем рисунке показаны примеры обоих видов вращения. И в том, и в другом случае квадрат попеременно поворачивается то в одну, то в другую сторону относительно своего центра, однако на нижнем рисунке увеличение угла поворота сопровождается увеличением протяженности фигуры в направлениях x и u. Нам кажется, что квадрат меняет форму, как будто его растягивают вдоль одной из диагоналей, одновременно прижимая к другой, однако в геометрии «Дихронавтов» он вращается как твердое тело, сохраняя неизменными любые расстояния между своими точками.

Следует также заметить, что в силу жесткой конструкции квадрата при вращении неизменными остаются не только длины его сторон, но и образуемые ими углы. И хотя нам и кажется, что углы по ходу вращения становятся то больше, то меньше, в действительности стороны квадрата все это время остаются перпендикулярными.

Световой и темновой конусы

Если световой импульс выпущен в момент времени t=0 из точки с координатами x=0, y=0, z=0, то расстояние, пройденное им к некоторому моменту времени t, в нашей Вселенной, как известно, будет равно произведению t на скорость света. Если вы выберем систему единиц стандартным образом, приняв скорость света равной 1, то пройденное расстояние будет в точности равно t. Обе величины останутся равными и после возведения в квадрат. Квадрат расстояния от начала координат до некоторой точки (x, y, z) равен x² + y² + z², и, следовательно:

или, что то же самое:

Чтобы получить аналогичное соотношение для вселенной «Дихронавтов», мы следуем привычному рецепту с заменой z² на –u². Таким образом, мировая линия светового импульса в мире «Дихронавтов» должна удовлетворять уравнению:

Так вот, хотя это уравнение описывает некоторое семейство кривых в полном, четырехмерном пространстве-времени, с его помощью мы также можем выяснить одну интересную особенность траекторий, по которым свет может двигаться в трехмерном пространстве «Дихронавтов». Если световой импульс выходит из начала координат в момент времени t=0, а затем, в некоторый момент t, оказывается в точке с координатами (x, y, u), то при отрицательном значении x² + y² – u² обратить x² + y² – u² – t² в нуль уже не получится, поскольку разность отрицательного и положительного (t²) чисел нулю равняться не может.

Отсюда следует, что в трехмерном пространстве «Дихронавтов» существует целое семейство направлений – а именно, удовлетворяющих соотношению

в пределах которых распространение света невозможно физически!

Эти запрещенные направления образуют конус, расходящийся от оси u под углом в 45 градусов. Конус не привязан к какой-то конкретной точке пространства; он описывает универсальное ограничение, касающееся направлений движения света. Таким образом, внутри этого конуса источники света ничего не излучают, а обычное зрение не работает.

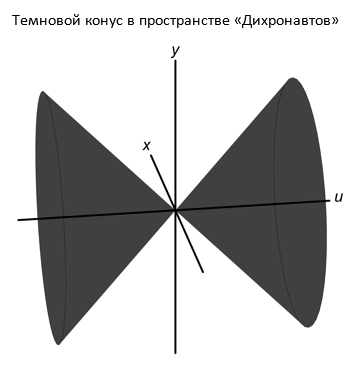
Мы привыкли думать, что если некоторому ограничению подчиняется даже свет, то оно же должно действовать и в отношении всех материальных объектов: например, зная, что свет не может покинуть черную дыру, мы автоматически приходим к выводу, что из нее не могут вырваться и обычные предметы, движущиеся с меньшей скоростью. Однако нет ничего более далекого от истины, когда речь идет о темновом конусе! Как мы уже видели в параграфе, посвященном мировым линиям, обычные тела не только способны двигаться параллельно оси u, но и могут делать это с совершенно произвольной скоростью.

Итак, хотя темновой конус лишен света, внутри него могут свободно перемещаться материальные объекты. А значит и звук, который представляет собой не что иное, как колебания материальных тел.

Падение вверх по склону

Предположим, что во вселенной «Дихронавтов» существует некий мир, на поверхности которого действует привычная нам гравитация. Подробное обсуждение потенциальной формы такого мира, а также особенностей действия гравитации в астрономических масштабах мы отложим до раздела «Мир «Дихронавтов»». Здесь же ограничимся допущением, что рассматриваемый нами участок поверхности достаточно мал, а ускорение свободного падения в его пределах постоянно и позволяет выделить одно из направлений в качестве «верха».

Направление «вверх» может оказаться как «пространственноподобным», так и «времениподобным»; при нашем выборе координатных обозначений оно, к примеру, может совпасть с осью x или u. Но так или иначе, среди пары пространственных направления, перпендикулярных «верху» – и, соответственно, находящихся в горизонтальной плоскости – должно найтись хотя бы одно, вид которого противоположен виду самого «верха». Что произойдет, если мы соорудим наклонную плоскость, высота которой увеличивается вдоль именно такого горизонтального направления противоположного вида, а затем поместим на нее некоторый объект и понаблюдаем, в какую сторону он начнет скользить?

Вопрос может показаться глупым, поскольку допускает всего один вариант ответа: вниз. Мы уже условились, что гравитация привычным нам образом притягивает тела к поверхности мира: если вы что-то уроните, этот предмет упадет вниз по прямой линии. Однако уронить предмет в воздухе – отнюдь не то же самое, что положить его на наклонную плоскость, дав ему возможность свободно скользить по ее поверхности: наклонная плоскость сама по себе воздействует на предмет с некоторой силой, которая добавляется к силе тяготения и меняет траекторию его движения.

Сила, с которой наклонная плоскость действует на предмет, будет перпендикулярна ее поверхности. Однако, как мы уже видели на примере с квадратом, углы которого приобретают странный вид при повороте в плоскости x–u, прямые, перпендикулярные в геометрии «Дихронавтов», вовсе не выглядят таковыми в евклидовом смысле.

На следующем рисунке мы видим предмет, расположенный на наклонной плоскости с углом в 30 градусов. Вес объекта (красная стрелка) тянет его вниз, в то время как сила реакции со стороны наклонной плоскости (синяя стрелка), не дающая предмету пробить ее насквозь, перпендикулярна ее поверхности. Величина силы реакции определяется тем фактом, что результирующая сила должна быть направлена вдоль поверхности наклонной плоскости – однако в данном случае суммарное усилие (зеленая стрелка) будет направлено к верхнему краю плоскости.

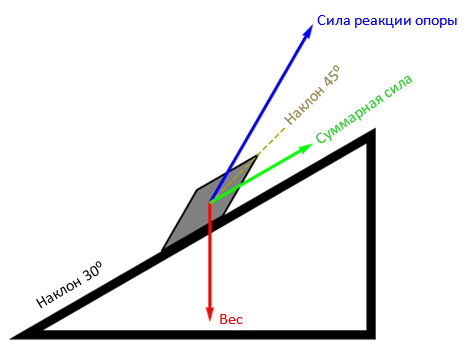
Хотя наши глаза отказываются верить в то, что сила реакции опоры перпендикулярна наклонной плоскости, в пространственной геометрии «Дихронавтов» это действительно так. Здесь отличительное свойство перпендикулярных линий заключается в том, что они образуют один и тот же угол с прямой, проходящей под углом 45⁰; угол между результирующей (параллельной поверхности наклонной плоскости) и силой реакции опоры, как нетрудно видеть, делится пополам штриховой линией на рисунке выше.

Таким образом, если трение о поверхность не сможет удержать предмет на одном месте, результирующая сила заставит его подниматься вверх по наклонной плоскости.

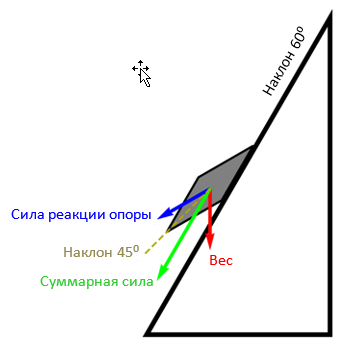
Ситуация, впрочем, меняется, если угол наклона плоскости становится больше 45 градусов. На рисунке ниже показана наклонная плоскость с углом 60⁰: дополнительного наклона оказывается достаточно, чтобы направить силу реакции опоры вниз. Под действием результирующей силы предмет начнет скользить вниз, причем его ускорение (если пренебречь силой трения) окажется даже больше, чем при простом падении в воздухе.

Может показаться, что первый случай со скольжением вверх по наклонной плоскости нарушает закон сохранения энергии – но все встает на свои места, если мы учтем поправки, которых требует определение энергии во вселенной «Дихронавтов».

Поскольку сила гравитации направлена вертикально вниз, потенциальную энергию тяготения мы будем определять, как величину, пропорциональную высоте тела над поверхностью мира, с некоторым положительным коэффициентом. Такое определение согласуется с положительным значением кинетической энергии вертикального движения. В этом плане ситуация ничем не отличается от поведения тел на поверхности Земли.

Но поскольку горизонтальная ось выбранной нами наклонной плоскости по своему виду противоположна направлению «вверх», кинетическая энергия вертикального движения будет отличаться от энергии горизонтального своим знаком. Если тело скользит по плоскости с углом наклона меньше 45 градусов, его горизонтальная скорость превышает вертикальную, поэтому суммарная кинетическая энергия будет отрицательной. Именно это и позволяет телу подниматься по наклонной плоскости, поскольку увеличение потенциальной энергии тяготения уравновешивается одновременным ростом отрицательной кинетической энергии.

Твердые тела, жидкости и коническая плазма

Отрицательная кинетическая энергия допускает ситуацию, при которой система материальных тел, не потребляя энергию извне, может, тем не менее, разогнаться до экстремально высоких скоростей – при условии, что их скорости изначально находятся «вблизи поверхности конуса», т. е. имеют примерно равные компоненты в пространственно- и времениподобных направлениях. Отсюда, в частности, следует, что даже если бы во вселенной «Дихронавтов» мог существовать идеальный газ (система частиц, взаимодействующих друг с другом только при непосредственном контакте), он был бы термодинамически нестабилен, поскольку случайные соударения частиц разгоняли бы их до неограниченно высоких скоростей.

Другим следствие этой же геометрии является тот факт, что величина (x₁ – x₂)^2 + (y₁ – y₂)^2 – (u₁ – u₂)^2 может быть крайне мала даже для двух частиц с совершенно разными координатами (x₁, y₁, u₁) и (x₂, y₂, u₂). Сила любого взаимодействия будет, как минимум отчасти, зависеть от этой величины. А значит, взаимодействия между частицами, находящимися на большом расстоянии с точки зрения индивидуальных координат, но при этом остающимися в окрестностях конусов друг друга, будут способствовать связыванию системы в единое целое, поэтому результат даже при низкой плотности вещества будет напоминать, скорее, жидкость, нежели газ.

Таким образом, материя «Дихронавтов», согласно нашим ожиданиям, может находиться в одном из трех агрегатных состояний: твердом, жидком и – если температура достаточно высока, либо плотность вещества достаточно мала, чтобы сила взаимодействия не смогла удержать частицы вместе – крайне нестабильной конфигурации, при которой скорости всех частиц находятся вблизи конуса. Последнее состояние мы будем называть «конической плазмой».