Чем грозит опрокидывание. Дополнительные материалы

Оригинал статьи:
https://www.gregegan.net/DICHRONAUTS/03/TopplingExtra.html

Ниже приводится ряд математических выкладок, дополняющих темы, описанные в статье «Чем грозит опрокидывание». Три пространственных измерения мы условимся обозначать буквами x, y, u, где координаты x, y соответствуют обычным, «пространственноподобным» измерениям, а u играет роль «времениподобной» оси. Это означает, что метрика g, определяющая скалярное произведение векторов, имеет вид:

$v \cdot w = g(v, w) = v_x w_x + v_y w_y - v_u w_u$

а квадрат модуля вектора, соответственно, выражается формулой:

$v \cdot v = g(v, v) = v_x^2 + v_y^2 - v_u^2$

Ось y мы выберем параллельной направлению «верх-низ», заданному силой тяготения, и будем считать, что движение интересующих нас тел ограничено плоскостью yu.

Приведенный ниже анализ исходит из допущения, что все объекты движутся достаточно медленно и не требуют привлечения релятивистской физики, а кинетическая энергия тела, имеющего массу m и скорость v, как следствие, выражается простой формулой K=mv²/2. Поэтому, говоря о силах и скоростях, «стремящихся к бесконечности», мы не утверждаем, что детали выведенных нами формул будут применимы для сколь угодно высоких скоростей. Впрочем, при столь резком росте сил, большинство реальных материалов разрушатся задолго до того, как дадут о себе знать какие бы то ни было релятивистские поправки.

Закрепленный стержень

Рассмотрим тонкий стержень длиной L и массой m, который, изначально находясь в вертикальном положении, падает так, что его нижняя точка не меняет своего положения. Если гиперболический угол наклона равен λ(t), положение точки стержня, находящейся на расстоянии s от его нижнего конца, можно выразить следующим уравнением:

$R(s, t) = s (\mathrm{sh} \lambda(t) e_u + \mathrm{ch} \lambda(t)e_y)$

где e_u и e_y – единичные векторы в направлении осей u и y, а в качестве начала координат выбран нижний конец стержня.

Полная потенциальная энергия стержня определяется интегралом произведения массы, высоты и гравитационного ускорения g по всей длине стержня; тот же результат можно получить, просто считая, что вся масса стержня сосредотпочена в его центре масс, s = L/2:

$U(t) = \cfrac{1}{2} Lmg \mathrm{ch} \lambda(t)$

Чтобы определить скорость произвольной точки стержня, достаточно продифференцировать R(s, t) по времени, что в итоге дает нам:

$v(s, t) = s \lambda'(t) \left( \mathrm{ch} \lambda(t) e_u + \mathrm{sh} \lambda(t) e_y \right)$

$v(s, t) \cdot v(s, t) = -s^2 \lambda'^2(t)$

Полная кинетическая энергия равна интегралу (m/2L) v(s, t) · v(s, t) ds , взятому по всей длине стержня, т.е.:

$K(t) = -\cfrac{1}{6} L^2 m \lambda'^2(t)$

Таким образом, полная энергия стержня, определяемая суммой кинетической и потенциальной, имеет вид:

$E(t) = \cfrac{1}{2} Lmg \mathrm{ch} \lambda(t) -\cfrac{1}{6} L^2 m \lambda'^2(t)$

и равна некоторой константе, зависящей от начальной угловой скорости стержня, λ‘(0), в вертикальном положении, при t=0 и λ(0)=0:

$E(0) = \cfrac{1}{2} Lmg - \cfrac{1}{6} L^2 m \lambda'^2(0)$

Воспользовавшись законом сохранения энергии, E(t) = E(0), имеем:

$\lambda'(t) = \sqrt{\lambda'^2(0) + \cfrac{3g}{L}(\mathrm{ch}\lambda - 1)}$

откуда также следует:

$\cfrac{\mathrm{d}t}{\mathrm{d}\lambda} = \cfrac{1}{\sqrt{\lambda'^2(0) + \cfrac{3g}{L}(\mathrm{ch}\lambda - 1)}}$

Решение последнего уравнения можно выразить через нормальный эллиптический интеграл Лежандра 1-го рода:

$t(\lambda) = -\cfrac{2i}{\lambda'(0)} F\left(\left. \cfrac{i\lambda}{2} \right| \cfrac{6g}{L\lambda'^2(0)}\right)$

где величина, стоящая после вертикальной черты под знаком F, представляет собой параметр эллиптического интеграла (равный квадрату его модуля), а i обозначает мнимую единицу. Значение t(λ), очевидно, должно быть действительным числом; применение функции F к мнимому аргументу также дает в результате мнимое число – умножая его на i, мы получаем в итоге действительный результат.

Таким образом, мы можем рассчитать t(λ) для произвольного λ, а затем, воспользовавшись численными методами, обратить полученную функцию и вычислить λ(t) для заданного момента t.

Продифференцировав по времени уравнение E(t) = E(0), мы получаем простое соотношение (в предположении, что λ’(t) ≠ 0):

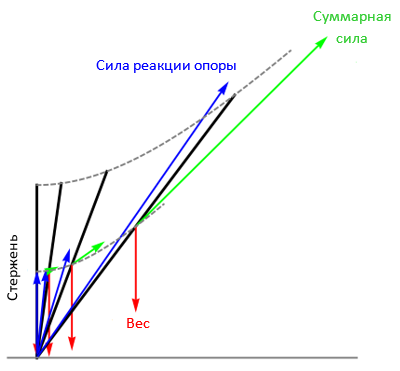
$\lambda''(t) = \cfrac{3g}{2L} \mathrm{sh} \lambda(t)$

Теперь мы можем рассчитать ускорение центра масс стержня, продифференцировав по времени v(L/2, t) и подставив полученные выше формулы для λ’(t) и λ”(t). Умножая это ускорение на массу стержня и вычитая фиксированный вектор веса, мы получаем силу реакции опоры, которая должна действовать на центр вращения стержня со стороны земли, чтобы обеспечить требуемое ускорение центра масс:

$F = \cfrac{m}{4} \left( \mathrm{sh}\lambda(t) \left( g(9 \mathrm{ch} \lambda(t) - 6) + 2L \lambda'^2(0) \right)e_u + (g (1 - 3 \mathrm{ch} \lambda(t))^2 + 2L \mathrm{ch} \lambda(t) \lambda'^2(0)) e_y \right)$

По мере падения стержня величина λ(t), как и обе компоненты силы реакции опоры, будут неограниченно возрастать.

Скользящий стержень

Рассмотрим снова тонкий стержень длиной L и массой m, изначально находящийся в вертикальном положении, но на этот раз позволим его нижнему концу свободно скользить по земле. При отсутствии трения сила реакции, с которой земля воздействует на стержень, – как и вес самого стержня – будет направлена строго по вертикали. Таким образом, если центр масс стержня изначально находится в состоянии покоя, его горизонтальная координата u будет оставаться неизменной, и мы можем ввести систему координат таким образом, чтобы стержень находился на уроне u = 0.

Если гиперболический угол наклона задается функцией λ(t), то положение точки стержня, удаленной на расстояние s от его основания, можно выразить формулой:

$R(s, t) = \left( s - \cfrac{L}{2} \right) \mathrm{sh} \lambda(t) e_u + s \mathrm{ch} \lambda(t) e_y$

Полная потенциальная энергия стержня, выраженная как функция λ(t), имеет тот же вид, что и в случае закрепленного стержня:

$U(t) = \cfrac{1}{2} Lmg \mathrm{ch} \lambda(t)$

Скорость произвольной точки стержня равна:

$v(s, t) = \lambda'(t) \left( \left( s - \cfrac{L}{2} \right) \mathrm{ch} \lambda(t) e_u + s \mathrm{sh} \lambda(t) e_y \right)$

$v(s, t) \cdot v(s, t) = - \left( s^2 + \cfrac{L}{4} (L - 4s) \mathrm{ch}^2 \lambda(t) \right) \lambda'^2(t)$

Суммарная кинетическая энергия определяется интегралом (m/2L) v(s, t) · v(s, t) ds, взятым по всей длине стержня:

$K(t) = -\cfrac{1}{24} L^2 m \lambda'^2(t) (4 - 3 \mathrm{ch}^2 \lambda(t))$

Последний множитель в этой формуле будет положительным при малых значениях λ(t), но меняет знак по достижении λ(t) = arch(2/√3) ≈ 0.549306. Отсюда следует, что по мере того, как λ(t) приближается к этому критическому значению, кинетическая энергия становится все менее чувствительной к изменениям λ’(t), и, следовательно, угловая скорость должна неограниченно возрастать только лишь для того, чтобы обеспечить постоянную величину кинетической энергии.

Полная энергия стержня, определяемая суммой кинетической и потенциальной, имеет вид:

$E(t) = \cfrac{1}{2} Lmg \mathrm{ch} \lambda(t) -\cfrac{1}{24} L^2 m \lambda'^2(t) (4 - 3 \mathrm{ch}^2 \lambda(t))$

и является постоянной величиной, которая зависит от начальной угловой скорости стержня, λ’(t), в вертикальном положении, при t=0 и λ(0)=0:

$E(0) = \cfrac{1}{2} Lmg - \cfrac{1}{24} L^2 m \lambda'^2(0)$

Используя закон сохранения энергии, E(t) = E(0), имеем:

$\lambda'(t) = \sqrt{\cfrac{\lambda'^2(0) + \cfrac{12g}{L}(\mathrm{ch} \lambda(t) - 1)}{4 - 3 \mathrm{ch}^2 \lambda(t)}}$

Отсюда можно получить формулу для dt/dλ, однако в отличие от стержня с закрепленным концом, соответствующее выражение, судя по всему, не позволяет получить замкнутую форму для t(λ). Тем не менее, с помощью численных методов можно найти как t(λ), так и λ(t).

Ускорение центра масс стержня можно, как и раньше, получить путем дифференцирования v(L/2, t) по времени. Умножая это ускорение на массу стержня и вычитая фиксированный вектор веса, мы получаем силу реакции опоры, необходимую для того, чтобы ускорение центр масс в точности соответствовало выведенной величине:

$F = m \left(\cfrac{2g(4 + 3 \mathrm{ch} \lambda(t) (\mathrm{ch} \lambda(t) - 2)) + L \mathrm{ch} \lambda(t) \lambda'^2(0)}{2 \left( 4 - 3 \mathrm{ch}^2 \lambda(t) \right)^2} \right) e_y$

Эта величина будет неограниченно возрастать при λ(t) → arch(2/√3) ≈ 0.549306.

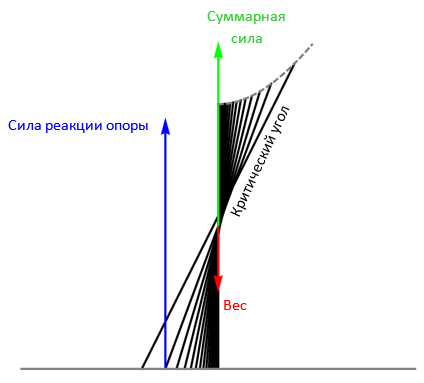
На рисунке ниже показаны последовательные положения стержня через равные интервалы времени, последнее из которых соответствует критическому углу, при котором действующие силы стремятся к бесконечности. Изображенные вектора сил соответствуют предшествующему положению стержня, для которого эти силы все еще выражаются конечными величинами.

Разрушающийся стержень

Заменив идеализированный тонкий стержень прямоугольной призмой, мы можем представить его в виде набора отдельных сегментов и рассчитать возникающие между ними сдвиговые силы. Рано или поздно эти силы станут достаточно большими, чтобы разрушить материал стержня.

Расчеты для случая падающей прямоугольной призмы практически повторяют аналогичные выкладки для рассмотренного ранее случая с закрепленным стержнем. Полная энергия в этом случае имеет вид:

$E(t) = \cfrac{1}{2} mg \left( L \mathrm{ch} \lambda(t) + w \mathrm{sh} \lambda(t) \right) - \cfrac{1}{6} \left( L^2 - w^2 \right) m \lambda'^2(t)$

где w – ширина призмы в направлении оси u. В итоге мы получаем чуть более сложную формулу угловой скорости:

$\lambda'(t) = \sqrt{\lambda'^2(0) + \cfrac{3g}{L^2 - w^2} \left( L(\mathrm{ch} \lambda(t) - 1) + w \mathrm{sh} \lambda(t) \right)}$

Если мы проинтегрируем величину, обратную λ’(t), представив, таким образом, время в качестве функции λ, результат также можно будет представить в замкнутой форме, хотя итоговое выражение окажется существенно сложнее аналогичной формулы для случая стержня и потребует использования гипергеометрических функций Аппеля. Так или иначе, мы можем представить силы и ускорения в виде функций одной переменной λ, вне зависимости от хода времени, который описывается зависимостью λ от t.

Ускорение произвольной точки призмы можно вычислить привычным способом, воспользовавшись приведенной выше формулой и ее производной; это даст нам возможность определить ускорение центра масс каждого сегмента и контактные силы, необходимые для объяснения той составляющей ускорения, которую невозможно списать исключительно на действие силы тяготения.

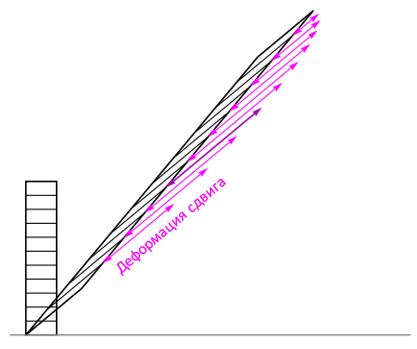
Упомянутые контактные силы можно разложить на силы, действующие по нормали, и силы сдвига; на рисунке ниже показана величина сдвиговых сил, которые в данном случае достигают максимума на уровне примерно 2/5 высоты призмы. По мере наклона призмы напряжения сдвига рано или поздно разорвут ее на части, и процесс будет повторяться с образовавшимися фрагментами до тех пор, пока они не станут слишком низкими, приобретя таким образом устойчивость к дальнейшему наклону.

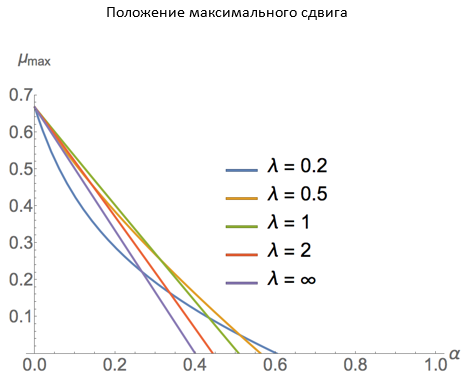
Более детально: если мы рассчитаем абсолютную величину сдвиговой силы, действующей на границе раздела сегментов, положение которой относительно основания составляет μ от полной длины призмы, то окажется, что она квадратично зависит от μ. Значение μ, при котором напряжение достигает максимальной величины, определяется соотношением:

$\mu_{\mathrm{max}} = \cfrac{(L^2 - w^2) (5g \mathrm{sh} \lambda - \lambda'^2(0) w) + 3gLw}{3gL (L \mathrm{sh} \lambda + w \mathrm{ch} \lambda)} - 1 = \cfrac{(1 - \alpha^2)(5 \mathrm{sh} \lambda - \lambda'^2(0)(w/g)) + 3\alpha}{3(\mathrm{sh} \lambda + \alpha \mathrm{ch} \lambda)} - 1$

где α = w/L. При λ = 0 эта величина отрицательна – а значит, максимальный сдвиг для малых λ будет достигаться при μ = 0. Если же λ велико, то результат можно аппроксимировать простой формулой:

$\lim_{\lambda \rightarrow \infty} \mu_{\mathrm{max}} = \cfrac{2 - 5 \alpha}{3}$

Если призма изначально имеет большую высоту и малую ширину, то ее первое разделение на две части произойдет при достаточно большом значении μ; так, при α = w/L = 1/5 и большом λ разлом случится на отметке μ ≈ 1/3. Но по мере уменьшения фрагментов и увеличения α максимум сдвиговых сил будет смещаться к основанию призмы, и в итоге от нее под действием силы реакции опоры начнут отделяться тонкие слои материала. Так будет продолжаться до тех пор, пока высота фрагментов призмы не уменьшится до уровня, при котором остановится их дальнейшее падение.

На следующем графике показана зависимость μ_max от α для некоторых значений λ в пределе с малым λ'(0), что позволяет пренебречь слагаемым λ‘²(0)w/g: