Рубрика: Дихронавты

Оригинал статьи:
https://www.gregegan.net/DICHRONAUTS/03/TopplingExtra.html

Ниже приводится ряд математических выкладок, дополняющих темы, описанные в статье «Чем грозит опрокидывание». Три пространственных измерения мы условимся обозначать буквами x, y, u, где координаты x, y соответствуют обычным, «пространственноподобным» измерениям, а u играет роль «времениподобной» оси. Это означает, что метрика g, определяющая скалярное произведение векторов, имеет вид:

а квадрат модуля вектора, соответственно, выражается формулой:

Ось y мы выберем параллельной направлению «верх-низ», заданному силой тяготения, и будем считать, что движение интересующих нас тел ограничено плоскостью yu.

Приведенный ниже анализ исходит из допущения, что все объекты движутся достаточно медленно и не требуют привлечения релятивистской физики, а кинетическая энергия тела, имеющего массу m и скорость v, как следствие, выражается простой формулой K=mv²/2. Поэтому, говоря о силах и скоростях, «стремящихся к бесконечности», мы не утверждаем, что детали выведенных нами формул будут применимы для сколь угодно высоких скоростей. Впрочем, при столь резком росте сил, большинство реальных материалов разрушатся задолго до того, как дадут о себе знать какие бы то ни было релятивистские поправки.

Закрепленный стержень

Рассмотрим тонкий стержень длиной L и массой m, который, изначально находясь в вертикальном положении, падает так, что его нижняя точка не меняет своего положения. Если гиперболический угол наклона равен λ(t), положение точки стержня, находящейся на расстоянии s от его нижнего конца, можно выразить следующим уравнением:

где e_u и e_y – единичные векторы в направлении осей u и y, а в качестве начала координат выбран нижний конец стержня.

Полная потенциальная энергия стержня определяется интегралом произведения массы, высоты и гравитационного ускорения g по всей длине стержня; тот же результат можно получить, просто считая, что вся масса стержня сосредотпочена в его центре масс, s = L/2:

Чтобы определить скорость произвольной точки стержня, достаточно продифференцировать R(s, t)  по времени, что в итоге дает нам:

Полная кинетическая энергия равна интегралу (m/2L) v(s, t) · v(s, t) ds , взятому по всей длине стержня, т.е.:

Таким образом, полная энергия стержня, определяемая суммой кинетической и потенциальной, имеет вид:

и равна некоторой константе, зависящей от начальной угловой скорости стержня, λ‘(0), в вертикальном положении, при t=0 и λ(0)=0:

Воспользовавшись законом сохранения энергии, E(t) = E(0), имеем:

откуда также следует:

Решение последнего уравнения можно выразить через нормальный эллиптический интеграл Лежандра 1-го рода:

где величина, стоящая после вертикальной черты под знаком F, представляет собой параметр эллиптического интеграла (равный квадрату его модуля), а i обозначает мнимую единицу. Значение t(λ), очевидно, должно быть действительным числом; применение функции F к мнимому аргументу также дает в результате мнимое число – умножая его на i, мы получаем в итоге действительный результат.

Таким образом, мы можем рассчитать t(λ) для произвольного λ, а затем, воспользовавшись численными методами, обратить полученную функцию и вычислить λ(t) для заданного момента t.

Продифференцировав по времени уравнение E(t) = E(0), мы получаем простое соотношение (в предположении, что λ’(t) ≠ 0):

Теперь мы можем рассчитать ускорение центра масс стержня, продифференцировав по времени v(L/2, t) и подставив полученные выше формулы для λ’(t) и λ”(t). Умножая это ускорение на массу стержня и вычитая фиксированный вектор веса, мы получаем силу реакции опоры, которая должна действовать на центр вращения стержня со стороны земли, чтобы обеспечить требуемое ускорение центра масс:

По мере падения стержня величина λ(t), как и обе компоненты силы реакции опоры, будут неограниченно возрастать.

Скользящий стержень

Рассмотрим снова тонкий стержень длиной L и массой m, изначально находящийся в вертикальном положении, но на этот раз позволим его нижнему концу свободно скользить по земле. При отсутствии трения сила реакции, с которой земля воздействует на стержень, – как и вес самого стержня – будет направлена строго по вертикали. Таким образом, если центр масс стержня изначально находится в состоянии покоя, его горизонтальная координата u будет оставаться неизменной, и мы можем ввести систему координат таким образом, чтобы стержень находился на уроне u = 0.

Если гиперболический угол наклона задается функцией λ(t), то положение точки стержня, удаленной на расстояние s от его основания, можно выразить формулой:

Полная потенциальная энергия стержня, выраженная как функция λ(t), имеет тот же вид, что и в случае закрепленного стержня:

Скорость произвольной точки стержня равна:

Суммарная кинетическая энергия определяется интегралом (m/2L) v(s, t) · v(s, t) ds, взятым по всей длине стержня:

Последний множитель в этой формуле будет положительным при малых значениях λ(t), но меняет знак по достижении λ(t) = arch(2/√3) ≈ 0.549306. Отсюда следует, что по мере того, как λ(t) приближается к этому критическому значению, кинетическая энергия становится все менее чувствительной к изменениям λ’(t), и, следовательно, угловая скорость должна неограниченно возрастать только лишь для того, чтобы обеспечить постоянную величину кинетической энергии.

Полная энергия стержня, определяемая суммой кинетической и потенциальной, имеет вид:

и является постоянной величиной, которая зависит от начальной угловой скорости стержня, λ’(t), в вертикальном положении, при t=0 и λ(0)=0:

Используя закон сохранения энергии, E(t) = E(0), имеем:

Отсюда можно получить формулу для dt/dλ, однако в отличие от стержня с закрепленным концом, соответствующее выражение, судя по всему, не позволяет получить замкнутую форму для t(λ). Тем не менее, с помощью численных методов можно найти как t(λ), так и λ(t).

Ускорение центра масс стержня можно, как и раньше, получить путем дифференцирования v(L/2, t) по времени. Умножая это ускорение на массу стержня и вычитая фиксированный вектор веса, мы получаем силу реакции опоры, необходимую для того, чтобы ускорение центр масс в точности соответствовало выведенной величине:

Эта величина будет неограниченно возрастать при λ(t) → arch(2/√3) ≈ 0.549306.

На рисунке ниже показаны последовательные положения стержня через равные интервалы времени, последнее из которых соответствует критическому углу, при котором действующие силы стремятся к бесконечности. Изображенные вектора сил соответствуют предшествующему положению стержня, для которого эти силы все еще выражаются конечными величинами.

Разрушающийся стержень

Заменив идеализированный тонкий стержень прямоугольной призмой, мы можем представить его в виде набора отдельных сегментов и рассчитать возникающие между ними сдвиговые силы. Рано или поздно эти силы станут достаточно большими, чтобы разрушить материал стержня.

Расчеты для случая падающей прямоугольной призмы практически повторяют аналогичные выкладки для рассмотренного ранее случая с закрепленным стержнем. Полная энергия в этом случае имеет вид:

где w – ширина призмы в направлении оси u. В итоге мы получаем чуть более сложную формулу угловой скорости:

Если мы проинтегрируем величину, обратную λ’(t), представив, таким образом, время в качестве функции λ, результат также можно будет представить в замкнутой форме, хотя итоговое выражение окажется существенно сложнее аналогичной формулы для случая стержня и потребует использования гипергеометрических функций Аппеля. Так или иначе, мы можем представить силы и ускорения в виде функций одной переменной λ, вне зависимости от хода времени, который описывается зависимостью λ от t.

Ускорение произвольной точки призмы можно вычислить привычным способом, воспользовавшись приведенной выше формулой и ее производной; это даст нам возможность определить ускорение центра масс каждого сегмента и контактные силы, необходимые для объяснения той составляющей ускорения, которую невозможно списать исключительно на действие силы тяготения.

Упомянутые контактные силы можно разложить на силы, действующие по нормали, и силы сдвига; на рисунке ниже показана величина сдвиговых сил, которые в данном случае достигают максимума на уровне примерно 2/5 высоты призмы. По мере наклона призмы напряжения сдвига рано или поздно разорвут ее на части, и процесс будет повторяться с образовавшимися фрагментами до тех пор, пока они не станут слишком низкими, приобретя таким образом устойчивость к дальнейшему наклону.

Более детально: если мы рассчитаем абсолютную величину сдвиговой силы, действующей на границе раздела сегментов, положение которой относительно основания составляет μ от полной длины призмы, то окажется, что она квадратично зависит от μ. Значение μ, при котором напряжение достигает максимальной величины, определяется соотношением:

   

где α = w/L. При λ = 0 эта величина отрицательна – а значит, максимальный сдвиг для малых λ будет достигаться при μ = 0. Если же λ велико, то результат можно аппроксимировать простой формулой:

Если призма изначально имеет большую высоту и малую ширину, то ее первое разделение на две части произойдет при достаточно большом значении μ; так, при α = w/L = 1/5 и большом λ разлом случится на отметке μ ≈ 1/3. Но по мере уменьшения фрагментов и увеличения α максимум сдвиговых сил будет смещаться к основанию призмы, и в итоге от нее под действием силы реакции опоры начнут отделяться тонкие слои материала. Так будет продолжаться до тех пор, пока высота фрагментов призмы не уменьшится до уровня, при котором остановится их дальнейшее падение.

На следующем графике показана зависимость μ_max от α для некоторых значений λ в пределе с малым λ'(0), что позволяет пренебречь слагаемым λ‘²(0)w/g:

Оригинал статьи:
https://www.gregegan.net/DICHRONAUTS/03/Toppling.html

В мире «Дихронавтов» вертикальному объекту, упавшему не в том направлении, грозит серьезная опасность. Если направление гравитационного верха/низа является пространственноподобным, то в горизонтальной плоскости будут располагаться как пространственноподобные, так и времениподобные направления, причем падение в пространственноподобном направлении – если таковое возможно – ничем не будет отличаться от падения в нашем мире. Такое падение можно назвать безопасным. Мы же хотим выяснить, что случится, если предмет – по какой бы то ни было причине – опрокинется в направлении противоположного рода, нежели верх/низ.

Подробности геометрии, лежащей в основе подобных сценариев, обсуждаются во вводной статье.

Читать далее Чем грозит опрокидывание

Оригинал статьи:
https://www.gregegan.net/DICHRONAUTS/01/WorldExtra.html

В этом разделе представлен ряд математических выкладок, дополняющих материалы предыдущего. Далее для обозначения пространственных координат мы будем использовать буквы x, y и u, где x и y представляю собой обычные, пространственноподобные направления, а направление u является времениподобным. Это означает, что метрика g, задающая скалярное произведение векторов, имеет вид:

а квадрат модуля произвольного вектора выражается формулой:

Читать далее Мир “Дихронавтов”. Дополнительные материалы

Оригинал статьи:
http://gregegan.net/DICHRONAUTS/01/World.html

Физика и геометрия вселенной «Дихронавтов», четыре измерения которой поровну делятся между временем и пространством, следуют довольно странным законам, с которыми читатель может познакомиться во вводной статье. Здесь же мы попытаемся в общих чертах описать мир, который мог бы существовать в такой вселенной. Мы намеренно не называем его «планетой», поскольку это слово имеет слишком много ассоциаций, относящихся к нашему собственному миру.

Далее мы будем обозначать три пространственных измерения буквами x, y, u, где координаты x, y соответствуют обычным, «пространственноподобным» измерениям, а u играет роль «времениподобной» оси. Это не означает, что u совпадает с координатой времени, которую мы обозначаем буквой t, а лишь выражает тот факт, что u может выступать в качестве переменной времени для другого наблюдателя, движение которого существенно отличается от нашего. Помимо прочего, «времениподобность» u означает, что квадрат трехмерного расстояния между точками (0, 0, 0) и (x, y, u) равен x² + y² – u², либо противоположной величине u² – x² – y², в зависимости от того, какая из них положительна. Более детальное объяснение этих понятий приводится во вводной статье.

Гравитация и форма мира

В нашей Вселенной крупный объект – будь то звезда или планета – под действием гравитации принимает форму, близкую к шарообразной. В случае идеального тела, обладающего точной сферической симметрией, сила тяготения всегда направлена к центру шара, а гравитационный потенциал одинаков во всех точках поверхности. Такая конфигурация является устойчивой – во всяком случае, до тех пор, пока внутренняя часть тела достаточна прочна, чтобы выдержать вес его внешних слоев.

Во вселенной «Дихронавтов» аналогом сферической поверхности служит гиперболоид. Эта поверхность имеет две разновидности, которые называются однополостным и двуполостным гиперболоидами (соответственно красный и зеленый на рисунке ниже). Первая напоминает бесконечную колбу песочных часов; вторая – пару бесконечных чаш, направленных в противоположные стороны. На рисунке бесконечную поверхность, по понятным причинам, можно изобразить лишь частично.

Нам потребуется твердое, трехмерное тело, поверхность которого состоит из одного или нескольких гиперболоидов. В геометрии «Дихронавтов» такое тело будет обладать идеальной симметрией относительно своего центра – по аналогии с тем, как сфера обладает идеальной симметрией в геометрии Евклида: внешний вид тела не будет меняться при повороте вокруг его центра. (Если это сбивает вас с толку, ознакомьтесь с вводным разделом «Геометрия и повороты в пространстве «Дихронавтов»».)

Такое тело будет иметь бесконечные размеры и обладать бесконечным объемом и массой. Мы можем мысленно обрезать гиперболоиды, получив в результате некоторое тело конечных размеров; это, конечно же, нарушит его идеальную симметрию, однако в случае физических объектов точная симметрия встречается довольно редко. У бесконечных, идеально симметричных версий, впрочем, есть свои преимущества, поскольку их проще описать математически; более того, до тех пор, пока все локально измеримые физические величины (как то сила тяготения или создаваемое внутри тела давление) остаются конечными, мы можем даже допустить существование подобных объектов в гипотетической вселенной «Дихронавтов».

Закономерность, которой подчиняется сила тяготения в нашей Вселенной, как известно, выражается законом обратных квадратов: сила взаимодействия двух материальных точек пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Во вселенной «Дихронавтов» вид этого закона не меняется – с той лишь разницей, что под «квадратом расстояния» теперь понимается x² + y² – u², если эта величина положительна, и противоположная величина, u² – x² – y², в противном случае.

Существует, понятное дело, и конус, на поверхности которого x² + y² – u² = 0, а, гравитационная сила, создаваемая 0-мерной точечной массой, достигает бесконечной величины. Это вызывает некоторое беспокойство – даже больше чем тот факт, что в нашей Вселенной гравитационная сила точечной массы стремится к бесконечности по мере приближения к центру притяжения.

С точки зрения микроскопических составляющих материи этот вывод указывает на то, что нам придется избегать частиц, буквально имеющих вид геометрических точек, заменяя их объектами, в которых масса (и, при наличии, электрический заряд) распределены по некоторой конечной области пространства. Но чтобы обойти эту проблему, нам вовсе не обязательно погружаться в детали физики частиц: как в нашей собственной Вселенной, так и в мире «Дихронавтов» закон тяготения можно легко представить в форме, где вместо масс отдельных частиц фигурирует плотность материи.

Во вселенной «Дихронавтов» соответствующее правило имеет вид:

Сумма вторых производных гравитационного потенциала по пространственноподобным координатам за вычетом второй производной по времениподобной координате равна произведению 4πG на плотность материи, где G – константа, описывающая силу гравитационного взаимодействия.

Как вы уже, должно быть, догадались, в случае с нашей Вселенной отличие состоит лишь в том, что вторые производные потенциала по трем пространственным координатам x, y, z входят в формулировку закона со знаком плюс; и ни одна – со знаком минус. Подобную формулировку ньютоновского закона можно интерпретировать как выражение геометрического свойства «силовых линий», позволяющих описывать гравитационное поле некоторого тела. По сути оно означает, что силовые линии могут начинаться и заканчиваться только на материальных частицах (но никак не в вакууме), а плотность распределения концов линий прямо пропорциональна плотности материи.

Другими словами, нам нужно найти гравитационный потенциал, удовлетворяющий этому закону для идеально симметричного распределения материи во вселенной «Дихронавтов». В качестве одного из вариантов мы могли бы взять одно- или двуполостный гиперболоид и заполнить пространство, ограниченное его поверхностью. Но тогда в некоторых направлениях нам придется иметь дело с бесконечно большим количеством материи.

Альтернативное решение – взять оба вида гиперболоидов и заполнить только пространство между ними, как показано на рисунке ниже. Этот объект также является бесконечным (хотя на картинке показан лишь его конечный фрагмент), но если мы выберем на поверхности одного из гиперболоидов произвольную малую область и рассмотрим объем находящегося под ним вещества, вплоть до центра мира, то этот объем окажется конечным и будет зависеть только от площади выбранной области и радиуса гиперболоида.

На следующем рисунке показан гравитационный потенциал, соответствующий такому распределению материи. На графике представлен срез в плоскости x–u, однако вид потенциала останется тем же самым и при любом повороте среза относительно оси u.

Сила тяготения, соответствующая такому потенциалу, всегда направлена к центру мира. Это может показаться удивительным, если учесть, что график отклоняется вниз по мере удаления от центра вдоль оси u; все дело в том, что тела, движущиеся во времениподобных направлениях, обладают отрицательной кинетической энергией, а значит, любой предмет, брошенный в этой области пространства, будет «катиться вверх», двигаясь в сторону увеличения потенциала. Таким образом, сила тяготения на всей поверхности гиперболоида – как одно-, так и двуполостного – имеет постоянную величину и всегда направлена к центру мира.

(Подробное описание математического выражения потенциала приводится в дополнительных материалах к статье).

Солнце, обитаемая зона и абсолютное лето

Какие миры могли бы возникнуть во вселенной с двумя пространственноподобными и двумя времениподобными измерениями? Ответ на этот вопрос зависит от особенностей космологии и строения материи. Материя во вселенной «Дихронавтов» труднее поддается математическому описания, чем наша собственная; предположив, что она состоит из точечных частиц, обладающих некоторым зарядом, мы обнаружим, что любая сила, стремящаяся к бесконечности по мере сокращения расстояния между частицами, будет иметь особые точки, в совокупности образующие целый конус с центром в данной частице (т. е. поверхность, в пределах которой расстояние до частицы равно нулю). В принципе мы могли бы распределить заряд по некоторой трехмерной области, не концентрируя его в одной точке пространства, что, в свою очередь, позволило бы нам избавиться от особенных точек. По сути именно так мы поступили в предыдущем разделе, когда речь шла о гравитационное поле. Однако для предсказания свойств, которыми могли бы обладать местные аналоги атомов и молекул, нам пришлось бы применить аппарат квантовой механики к отдельным, протяженным объектам, находящимся в пространстве с принципиально иной геометрией, нежели геометрия нашей Вселенной, что потребовало бы отнюдь не тривиальных усилий.

Поэтому, вместо того, чтобы заниматься детальной проработкой физики частиц, химии и космологической истории вселенной «Дихронавтов», мы ограничимся схематичным описанием одного из возможных миров, а также некоторых свойств материи, необходимых для его функционирования.

Представим себе большой гиперболоидальный мир из твердого материала. Как уже было сказано в предыдущем разделе, даже при бесконечных размерах самого мира сила тяготения в любой точке его поверхности имеет одно и то же, конечное значение и всегда направлена к центру мира.

Если твердая поверхность со всех сторон окружена некой «атмосферой», то по своим свойствам такая атмосфера будет напоминать не газ, а жидкость – причины этого мы обсуждали во вводной статье. В мире романа такая атмосфера действительно присутствует, но при этом является достаточно разреженной и прозрачной в оптической части спектра, чтобы персонажи книги воспринимали ее примерно так же, как мы сами воспринимаем наш воздух. Выражение «разреженная жидкость» звучит довольно странно, однако благодаря дальнодействующим силам, направленным вдоль конуса каждой из частиц, термодинамические свойства жидкости может проявлять даже система сравнительно низкой плотности.

Что будет происходить на границе между такой жидкостью и космическим вакуумом? Даже не зная всех деталей межмолекулярного взаимодействия, возможные варианты можно поделить на две группы: либо жидкость сохраняет целостность, как это имеет место с некоторыми твердыми телами при контакте с вакуумом, либо претерпевает резкий фазовый переход в состояние «конической плазмы», при котором частицы разгоняются до высоких скоростей за счет случайных соударений.

На роль атмосферы нам понадобится жидкость первого типа, которая может спокойно контактировать с вакуумом, герметизируясь за счет своей собственной вязкости. Второй же вариант позволяет некоторым скоплениям жидкости выступать в роли источника света и тепла. Иначе говоря, в качестве «звезд». В нашей вселенной звезды должны обладать некоторой минимальной массой, при которой в их ядре возникает давление, достаточно для запуска термоядерных реакций. В то время как во вселенной «Дихронавтов» звезде достаточно просто состоять из жидкости подходящего типа.

Компанию гиперболоидальному миру «Дихронавтов» (показанному на следующем рисунке) составляет миниатюрная звезда, которая движется вокруг него по компактной круговой орбите. Это явно не единственная возможная конфигурация, однако разительные отличия от нашего собственного мира вкупе с возникающими в подобной ситуации экзотическими эффектами местной геометрии, куда больше благоприятствуют интересному повествованию, нежели рассказ об очередной планете, обращающейся вокруг далекой и громадной звезды.

Как уже упоминалось ранее, любой источник света во вселенной «Дихронавтов» характеризуется «темновым» конусом, внутри которого не излучается свет. Таким образом, освещенная солнцем часть поверхности ограничена с двух сторон. Помимо этого существует привычная нам граница между ночью и днем. Однако даже находясь на дневной стороне и двигаясь к северу или югу от окружности, расположенной строго под орбитой солнца, вы рано или поздно оказываетесь в его темновом конусе.

Может показаться, что жизнь к северу или югу от окружностей, образованных пересечением темнового конуса с поверхностью мира, будет отличаться всего лишь одним любопытным феноменом, при котором свет исчезает в районе полудня, а продолжительность этого дневного «затмения» растет с увеличением широты. Но именно здесь геометрия проявляет себя с неприглядной стороны. Вблизи темнового конуса солнца расстояние между поверхностью звезды и поверхностью мира стремится к нулю, а интенсивность солнечного излучения, как следствие, достигает колоссальных величин. Оказаться в месте, где подобные – пусть и кратковременные – вспышки происходят дважды в день, – все равно что подписать себе смертный приговор. Таким образом, эти окружности служат границей территории, которая в романе именуется абсолютным летом – так называются области, в которых расстояние от Солнца время от времени падает до нуля, и выживание становится попросту невозможным.

Если на нашей планете высокие широты коррелируют с прохладной погодой, то в мире «Дихронавтов» самым холодным местом будет пояс, расположенный в точности под орбитой солнца – так называемый средизимний круг. Все остальные точки, согласно геометрии их вселенной, будут, наоборот, располагаться ближе к солнцу, если измерять расстояние ровно в полдень. К северу и югу от средизимнего круга располагается обитаемая зона, в пределах которой температура благоприятствует развитию жизни. Граница этой зоны проходит на довольно ощутимом расстоянии от начала абсолютного лета и располагается там, где вода (не в нашем понимании, а в смысле общедоступного растворителя, играющего сходную роль в биохимии «Дихронавтов») из-за высокой температуры начинает слишком быстро растворяться в жидкой атмосфере, оставляя после себя лишь пересохшую землю.

На рисунке выше границы обитаемой зоны отмечены двумя голубыми полосами мелководных болот, где температура опускается до отметки, при которой влага, заключенная в более горячем воздухе к северу и югу, начинает выпадать на землю в виде дождя.

Зернистость земли и миграция

Представьте, что мы расположили множество геометрических фигур в виде сетки, а затем нарисовали на каждой из них стрелку, указывающую в одном и том же направлении. Дадим этим фигурам возможность свободно вращаться на плоскости, ограничивая их движение лишь тем фактом, что при слишком большом повороте они могут столкнуться с кем-то из своих соседей. Если фигуры расположены не слишком плотно, то в евклидовом пространстве ориентация их стрелок может оказаться совершенно случайной, как показано на следующем рисунке:

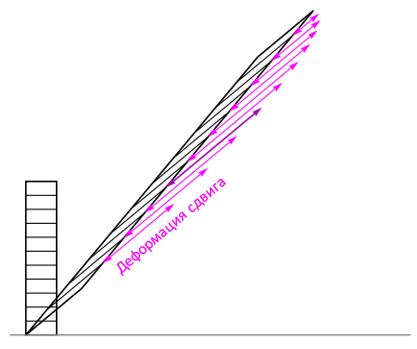
Если же аналогичную конфигурацию представить в пространстве «Дихронавтов» – так, чтобы одно из направлений в плоскости сетки было пространственноподобным, а другое – времениподобным, – то растяжение фигур в процессе их вращения приведет к тому, что они будут сталкиваться со своими соседями даже при поворотах на очень малые углы, что в итоге даст картину, напоминающую рисунок ниже:

Несмотря на некоторую надуманность, приведенный выше пример неплохо демонстрирует один общий принцип: на поверхности однополостного гиперболоида – где в горизонтальной плоскости имеется как пространственно-, так и времениподобное направление, – земля будет проявлять четко выраженную направленную зернистость, которая не наблюдается на нашей планете.

Несмотря на некоторую надуманность, приведенный выше пример неплохо демонстрирует один общий принцип: на поверхности однополостного гиперболоида – где в горизонтальной плоскости имеется как пространственно-, так и времениподобное направление, – земля будет проявлять четко выраженную направленную зернистость, которая не наблюдается на нашей планете.

Оказавшись пасмурной ночью в незнакомой точке нашей планеты, и имея при себе лишь мощный источник искусственного освещения, позволяющий во всех подробностях изучить внешний вид ландшафта, вы бы ни за что не смогли определить, где именно находится север и юг, а где – восток и запад. Нет никакой причины, из-за которой подобная информация непременно должна найти отражение в геологических особенностях Земли. Однако на поверхности однополостного гиперболоида имеет место не только фундаментальное различие между осями север-юг и восток-запад (так, световое зрение не работает в пределах сорока пяти градусов от направлений на север и юг): даже отдельные песчинки не могут располагаться под углами, которые заметно отличаются от их соседей, так как попытавшись принять собственную, непохожую на остальных ориентацию, они бы встретились с сопротивлением окружающих песчинок.

Мы описали гиперболоидальный мир «Дихронавтов» как идеально симметричную фигуру – остающуюся неизменной при любом повороте вокруг ее центра – однако это, понятное дело, верно лишь для идеализированной модели гладкого и однородного мира, которая годится для расчетов гравитационного поля, но никак не для ответа на вопрос: каково это – ходить по его поверхности? Как и наша Земля, мир «Дихронавтов» будет обладать сложным рельефом гор и долин. Но если исследователь практически в любой точке Земли может свободно повернуться на все триста шестьдесят градусов – если, конечно, он не стоит на узеньком уступе горы или пытается пролезть сквозь запредельно тесную расщелину, – то тела существ, обитающих в мире «Дихронавтов» вынуждены подчиняться особенностям местной геологии. Если вы находитесь на обширной и плоской равнине, где нет никого, кроме вас, все эффекты вращения будут ограничены лишь чисто геометрическим правилом, согласно которому ни один поворот не может превратить пространственноподобное направление во времениподобное и наоборот; но как только на поверхности появляются какие-либо препятствия, столкновение с ними будет препятствовать вашему движению, поэтому в большинстве случаев перемещение против зернистости рельефа будет сильно затруднено или вовсе окажется невозможным.

Другими словами, мир «Дихронавтов» следует представлять не в виде однообразного гиперболоида, а как объект с нанесенной на него сеткой геологических координат, где долгота отсчитывается вокруг гиперболоида, а широта – вверх и вниз от заранее выбранной экваториальной окружности. Но если координаты, которыми мы пользуемся на Земле, привязаны к полюсам вращения, то отсчет дней во вселенной «Дихронавтов» объясняется вовсе не обращением мира вокруг какой-либо оси, не говоря уже о том, что единственной оси симметрии у него попросту нет – точно так же, как нет ее и у сферы. (Такая ось появляется, когда мы пытаемся изобразить мир «Дихронавтов» в евклидовом пространстве, но это всего лишь побочный эффект геометрии, которую мы используем для его визуализации.) Это позволяет выбирать геологические координаты в соответствии с зернистостью ландшафта: геологический север, юг, восток и запад – это (усредненные) направления, по которым можно сориентировать стороны квадратной коробки так, чтобы она не цеплялась за другие предметы. На Земле подобное определение было бы бесполезным, ведь такую коробку можно развернуть как угодно. Однако в мире «Дихронавтов» поворот квадрата сопряжен с известным риском.

Конечно, есть и другая система естественных координат – а именно, та, что связана с движением солнца. Очевидным кандидатом на роль экватора в солнечных координатах является средизимняя окружность, расположенная на поверхности мира строго под орбитой солнца.

Должны ли обе системы обозначения широты и долготы быть каким-то образом согласованы друг с другом? Ничто не мешает нам вообразить, что мир возник одновременно с солнцем, а их системы координат были согласованы благодаря тому, что оба тела изначально находились в одних и тех же условиях. Но с тем же успехом можно представить и сценарий, в котором они сформировались совершенно независимо друг от друга.

В сюжете романа возникает еще одно осложнение: несмотря на то, что в далеком прошлом геологические и солнечные координаты действительно могли совпадать друг с другом, соотношение между ними менялось на протяжении целых эпох. Вопрос о том, испытывает ли мир медленное вращение относительно фиксированной орбиты солнца, или же орбита самого солнца медленно наклоняется по отношению к неподвижному миру, является предметом договоренности, однако конечный эффект и в том, и в другом случаях будет одинаковым: обитаемая зона непрерывно смещается по поверхности мира, заставляя людей перебираться с места на места в ходе медленной, но постоянной миграции.

Далее мы в целях удобства будем исходить из того, что вращается сам мир. Поскольку такое вращение охватывает одно пространственноподобное и одно времениподобное измерения, его поведение отличается от кругового, периодического движения, которое, к примеру, совершает обращающееся по орбите солнце.

На следующем рисунке представлены два ракурса гиперболоида (с фиксированной красно-синей сеткой геологических координат), который в процессе вращения теряет синхронность с солнечными координатами (показаны серым цветом). Обитаемая зона, привязанная к сетке солнечных координат, выделена зеленым цветом.

В случае с левым рисунком наблюдатель находится лицом к одной из узловых точек – которые остаются неизменными в процессе поворота, – в то время как правый повернут относительно левого на девяносто градусов.

Вблизи узловых точек эффект по сути сводится к двумерному повороту поверхности вокруг самого узла. Если бы наблюдатель, стоя в таком месте, попытался сохранить свою ориентацию относительно окружающего ландшафта, то равно или поздно его тело так сильно развернулось бы по отношению к обитаемой зоне, что попросту вышло бы за ее пределы, оказавшись в области абсолютного лета. Или, если описывать происходящее с точки зрения самого наблюдателя, обитаемая зона бы сжалась настолько, что ее размер по одной из осей стал бы меньше его собственного тела. Если бы земля была идеально плоской и гладкой, наблюдатель мог бы спастись, поворачиваясь так, чтобы его тело сохраняло постоянную ориентацию относительно обитаемой зоны. Однако в условиях реалистичного ландшафта это рано или поздно станет невозможным.

В девяноста градусах от узловой точки проблема исчезает. Несмотря на то, что земля продолжает двигаться на север по отношению к солнцу, вынуждая жителей мигрировать на юг, чтобы все время оставаться в пределах обитаемой зоны, определения осей запад-восток/север-юг с точки зрения геологических и солнечных координат остаются согласованными друг с другом.

Так вот, где-то между этими точками рассогласование солнечных и геологических координат начнет вызывать определенные проблемы. Ключевой вопрос заключается в том, будет ли безопасная полоса земли в пределах обитаемой зоны сжиматься до бесконечности, или же устремится к некоторому минимальному значению, вблизи которого будет по сути оставаться неизменной на протяжении целых эр.

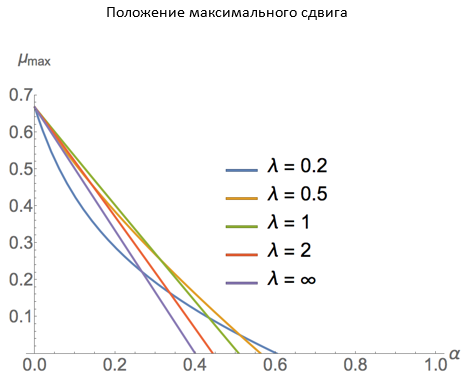
Ответом на этот вопрос служит изображенный ниже график, который дает обитателям «Дихронавтов» повод для оптимизма. Кривая показывает, как в зависимости от долготы (рассчитанной относительно одной из узловых точек) меняется характеристика поворота, измеряющего разницу между геологическими и солнечными координатами. Серые кривые соответствуют различным значениям этого параметра в самой узловой точке, красная – отражает предельное состояние, при котором характеристика узловой точки стремится к бесконечности. Предельная кривая демонстрирует тот факт, что на поверхности мира всегда найдется достаточно протяженный интервал долготы, внутри которого относительное вращение не слишком велико, а у обитающих в нем людей всегда есть возможность сориентировать свое тело согласно локальной зернистости земли, не рискуя выйти за границы обитаемой зоны.

(Детальное описание выкладок, лежащих в основе этого графика, приводится в дополнительных материалах к статье.)

– Я пригласил вас, чтобы обсудить перспективы дальнейшей работы, – начал Джонас. – Ваша служба в Бюро Топографии достойна всяческих похвал, и я рад сообщить, что мы готовы предложить вам целых три варианта на выбор.

– Почту за честь, – сказал в ответ Тео. Сэт сопроводил его слова неуклюжим кивком, желая показать, что разделяет те же чувства. Однако наблюдения с аэростата стали возможными, именно благодаря изобретательности Тео, и именно с ним директор хотел обсудить грандиозные планы насчет будущего миграции. Во время подобных встреч Сэту хотелось стать таким же незаметным, как поперечник самого Джонаса, который вел себя настолько сдержанно, что Сэт даже не знал его имени.

Читать далее Дихронавты. Глава 12

Сэт проснулся рано, но, зная, что уже вряд ли уснет, решил выйти на предутреннюю прогулку и размять ноги прежде, чем его настигнет удручающая дневная жара. На обратном пути небо посветлело настолько, что он увидел лагерь целиком – раскинувшееся перед его глазами лоскутное одеяло из клочков грубой ткани, закрепленных на пыльном склоне холма.

– Здесь, наверное, две сотни палаток, – сообразил он. – Когда это произошло?

– Ну ты же знаешь поговорку, – сказал в ответ Тео. – Чтобы вырастить топографа, нужна целая деревня.

Читать далее Дихронавты. Глава 11

К западу и востоку от границы парников, насколько хватало глаз, протянулась узкая полоска зелени. На севере располагались бесплодные, открытые всем ветрам пески, на юге – обширные пространства, покрытые иссохшей грязью, где дождь по ночам выдалбливал в земле лунки, а днем бесследно исчезал под палящим зноем. Но сейчас прямо перед ними в густой траве змеились сотни крошечных, сверкающих в свете Солнца, ручейков.

Чем ближе подбиралась экспедиция, тем большее воодушевление чувствовал Сэт при виде этого гигантского зеленого коридора. Конечно, ручейки, которые он мог охватить взглядом, пересыхали, стоило им только углубиться в пустыню, ведь их течение ветвилось на слишком мелкие, разбегавшиеся в разных направлениях, струйки. Но часто ли погоде и ландшафту, действуя заодно, удавалось объединить эти водяные ниточки, превратив их в нечто более живучее?

Читать далее Дихронавты. Глава 10

Когда наступила ночь, они разбили в пустыне лагерь позади невысокого, осыпающегося выступа скалы – вне поля зрения людей, которые направлялись из леса непосредственно в город или обратно.

Сэт старался сохранять объективность, не поддаваясь каким-либо теориям насчет связи жителей города с исчезновением его друзей. По-прежнему оставался риск несчастного случая, но даже если местные сыграли в произошедшем какую-то роль, это еще не доказывало, что они действовали с дурными намерениями. Горожане вполне могли наткнуться на лежащих без сознания топографов где-нибудь в джунглях и доставили их в город, чтобы оказать медицинскую помощь.

Читать далее Дихронавты. Глава 9

Первыми до места встречи добрались Сэт и Тео. Осмотрев небольшой скальный выступ в поисках треугольника, который Райна вырезала на одной из его сторон в качестве опознавательного знака, Сэт снял рюкзак и уселся на теплый камень, свесив голову вниз, чтобы следить за остальными.

Читать далее Дихронавты. Глава 8

– Похоже, мы идем не туда, – с мрачной категоричностью заявила Райна.

Амир наклонил голову и посмотрел на свой теневой визир. – Мы ушли слишком далеко на север или слишком далеко на юг? – спросил Азиз.

– Точно не скажешь, – ответила Райна.

Читать далее Дихронавты. Глава 7